Class for stock-recruitment models.
Usage
FLSR(model, ...)
# S4 method for ANY
FLSR(model, ...)
# S4 method for missing
FLSR(model, ...)Details
A series of commonly-used stock-recruitment models are already available,
including the corresponding likelihood functions and calculation of initial
values. See SRModels for more details and the exact
formulation implemented for each of them.
Slots
- name
Name of the object (
character).- desc
Description of the object (
character).- range
Range (
numeric).- rec
Recruitment series (
FLQuant).- ssb
Index of reproductive potential, e.g. SSB or egg oor egg production (
FLQuant).- fitted
Estimated values for rec (
FLQuant).- residuals
Residuals obtained from the model fit (
FLArray).- covar
Covariates for SR model (
FLQuants).- model
Model formula (
formula).- gr
Function returning the gradient of the likelihood (
function).- logl
Log-likelihood function (
function).- initial
Function returning initial parameter values for the optimizer (
function).- params
Estimated parameter values (
FLPar).- logLik
Value of the log-likelihood (
logLik).- vcov
Variance-covariance matrix (
array).- details
Extra information on the model fit procedure (
list).- logerror
Is the error on a log scale (
logical).- distribution
(
factor).- hessian
Resulting Hessian matrix from the fit (
array).
Examples
# Create an empty FLSR object.
sr1 <- FLSR()
# Create an FLSR object using the existing SR models.
sr2 <- FLSR(model = 'ricker')
sr2@model
#> rec ~ a * ssb * exp(-b * ssb)
#> <environment: 0x558842cbec30>
sr2@initial
#> function(rec, ssb) {
#> # The function to provide initial values
#> res <-coefficients(lm(log(c(rec)/c(ssb))~c(ssb)))
#> return(FLPar(a=max(exp(res[1])), b=-max(res[2])))}
#> <bytecode: 0x558842cca2f0>
#> <environment: 0x558842cbec30>
#> attr(,"lower")
#> [1] -Inf -Inf
#> attr(,"upper")
#> [1] Inf Inf
sr2@logl
#> function(a, b, rec, ssb)
#> loglAR1(log(rec), log(a*ssb*exp(-b*ssb)))
#> <bytecode: 0x558842ccbd40>
#> <environment: 0x558842cbec30>
sr3 <- FLSR(model = 'bevholt')
sr3@model
#> rec ~ a * ssb/(b + ssb)
#> <environment: 0x5588424ffef0>
sr3@initial
#> function(rec, ssb) {
#> a <- max(quantile(c(rec), 0.75, na.rm = TRUE))
#> b <- max(quantile(c(rec)/c(ssb), 0.9, na.rm = TRUE))
#> return(FLPar(a = a, b = a/b))}
#> <bytecode: 0x55884250acf0>
#> <environment: 0x5588424ffef0>
#> attr(,"lower")
#> [1] -Inf -Inf
#> attr(,"upper")
#> [1] Inf Inf
sr3@logl
#> function(a, b, rec, ssb)
#> loglAR1(log(rec), log(a*ssb/(b+ssb)))
#> <bytecode: 0x55884250e6d0>
#> <environment: 0x5588424ffef0>
# Create an FLSR using a function.
mysr1 <- function(){
model <- rec ~ a*ssb^b
return(list(model = model))}
sr4 <- FLSR(model = mysr1)
# Create an FLSR using a function and check that it works.
mysr2 <- function(){
formula <- rec ~ a+ssb*b
logl <- function(a, b, sigma, rec, ssb) sum(dnorm(rec,
a + ssb*b, sqrt(sigma), TRUE))
initial <- structure(function(rec, ssb) {
a <- mean(rec)
b <- 1
sigma <- sqrt(var(rec))
return(list(a=a, b=b, sigma=sigma))},
lower = c(0, 1e-04, 1e-04), upper = rep(Inf, 3))
return(list(model = formula, initial = initial, logl = logl))
}
ssb <- FLQuant(runif(10, 10000, 100000))
rec <- 10000 + 2*ssb + rnorm(10,0,1)
sr5 <- FLSR(model = mysr2, ssb = ssb, rec = rec)
sr5.mle <- fmle(sr5)
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = 163406.701688
#> Scaled convergence tolerance is 0.00243495
#> Stepsize computed as 7496.820439
#> BUILD 4 9181163641994.675781 141540.160296
#> LO-REDUCTION 6 2129977522396.011719 141540.160296
#> HI-REDUCTION 8 538828068094.632690 141540.160296
#> HI-REDUCTION 10 135471725247.814880 141540.160296
#> HI-REDUCTION 12 33943657773.507915 141540.160296
#> HI-REDUCTION 14 8485095365.236800 141540.160296
#> HI-REDUCTION 16 2116059492.850708 141540.160296
#> HI-REDUCTION 18 525861882.708607 141540.160296
#> HI-REDUCTION 20 129877061.405528 141540.160296
#> HI-REDUCTION 22 31729980.268444 141540.160296
#> HI-REDUCTION 24 7626132.270864 141540.160296
#> HI-REDUCTION 26 1817676.813873 141540.160296
#> HI-REDUCTION 28 474446.919157 141540.160296
#> HI-REDUCTION 30 219409.298128 141540.160296
#> REFLECTION 32 193097.769001 128665.987280
#> LO-REDUCTION 34 163406.701688 128665.987280
#> EXTENSION 36 141540.160296 86398.126977
#> LO-REDUCTION 38 136930.633178 86398.126977
#> HI-REDUCTION 40 128665.987280 86398.126977
#> EXTENSION 42 99061.935418 57313.041709
#> LO-REDUCTION 44 97008.208272 57313.041709
#> EXTENSION 46 86398.126977 31904.956474
#> REFLECTION 48 61527.247440 31099.754288
#> HI-REDUCTION 50 57313.041709 31099.754288
#> EXTENSION 52 41725.116784 9994.304172
#> LO-REDUCTION 54 31904.956474 9994.304172
#> EXTENSION 56 31099.754288 7899.295274
#> EXTENSION 58 16622.579730 2362.855801
#> REFLECTION 60 9994.304172 865.531551
#> HI-REDUCTION 62 7899.295274 865.531551
#> LO-REDUCTION 64 2362.855801 697.123217
#> LO-REDUCTION 66 2061.396804 131.370456
#> HI-REDUCTION 68 865.531551 131.370456
#> LO-REDUCTION 70 697.123217 131.370456
#> HI-REDUCTION 72 300.924786 131.370456
#> HI-REDUCTION 74 157.736501 121.566363
#> HI-REDUCTION 76 141.827460 73.447339
#> LO-REDUCTION 78 131.370456 72.115881
#> HI-REDUCTION 80 121.566363 72.115881
#> LO-REDUCTION 82 86.968056 72.115881
#> HI-REDUCTION 84 80.304614 72.115881
#> LO-REDUCTION 86 74.328873 72.115881
#> HI-REDUCTION 88 73.447339 71.407375
#> HI-REDUCTION 90 72.905934 70.943981
#> LO-REDUCTION 92 72.115881 70.785005
#> HI-REDUCTION 94 71.407375 70.785005
#> HI-REDUCTION 96 71.092687 70.785005
#> HI-REDUCTION 98 70.943981 70.785005
#> HI-REDUCTION 100 70.917673 70.763889
#> LO-REDUCTION 102 70.829585 70.752861
#> HI-REDUCTION 104 70.785005 70.752861
#> HI-REDUCTION 106 70.763889 70.749545
#> REFLECTION 108 70.761302 70.748467
#> REFLECTION 110 70.752861 70.744787
#> HI-REDUCTION 112 70.749545 70.740893
#> EXTENSION 114 70.748467 70.724123
#> HI-REDUCTION 116 70.744787 70.724123
#> LO-REDUCTION 118 70.740893 70.724123
#> EXTENSION 120 70.734920 70.722481
#> LO-REDUCTION 122 70.734458 70.722481
#> EXTENSION 124 70.724123 70.695721
#> LO-REDUCTION 126 70.723645 70.695721
#> LO-REDUCTION 128 70.722481 70.695721
#> EXTENSION 130 70.715444 70.676064
#> EXTENSION 132 70.703208 70.637697
#> LO-REDUCTION 134 70.695721 70.637697
#> EXTENSION 136 70.676064 70.611820
#> EXTENSION 138 70.644578 70.541271
#> LO-REDUCTION 140 70.637697 70.541271
#> LO-REDUCTION 142 70.611820 70.541271
#> EXTENSION 144 70.563786 70.443727
#> LO-REDUCTION 146 70.552506 70.443727
#> EXTENSION 148 70.541271 70.403008
#> EXTENSION 150 70.455309 70.266001
#> LO-REDUCTION 152 70.443727 70.266001
#> LO-REDUCTION 154 70.403008 70.266001
#> LO-REDUCTION 156 70.347710 70.266001
#> EXTENSION 158 70.325720 70.207409
#> EXTENSION 160 70.281998 70.174752
#> EXTENSION 162 70.266001 69.966123
#> LO-REDUCTION 164 70.207409 69.966123
#> LO-REDUCTION 166 70.174752 69.966123
#> EXTENSION 168 70.102607 69.665746
#> EXTENSION 170 70.010629 69.402631
#> LO-REDUCTION 172 69.966123 69.402631
#> EXTENSION 174 69.665746 68.343674
#> LO-REDUCTION 176 69.467717 68.343674
#> EXTENSION 178 69.402631 67.340172
#> EXTENSION 180 68.578834 63.479393
#> LO-REDUCTION 182 68.343674 63.479393
#> Warning: NaNs produced
#> HI-REDUCTION 184 67.340172 63.479393
#> Warning: NaNs produced
#> REFLECTION 186 66.915483 61.301086
#> Warning: NaNs produced
#> HI-REDUCTION 188 65.241403 61.301086
#> HI-REDUCTION 190 64.548113 61.301086
#> LO-REDUCTION 192 64.162698 61.301086
#> EXTENSION 194 63.479393 58.547281
#> Warning: NaNs produced
#> REFLECTION 196 62.922467 58.529138
#> Warning: NaNs produced
#> HI-REDUCTION 198 61.301086 58.529138
#> LO-REDUCTION 200 61.266886 58.529138
#> Warning: NaNs produced
#> HI-REDUCTION 202 59.761060 58.529138
#> Warning: NaNs produced
#> REFLECTION 204 58.630956 56.896382
#> LO-REDUCTION 206 58.547281 56.896382
#> Warning: NaNs produced
#> HI-REDUCTION 208 58.529138 56.896382
#> REFLECTION 210 57.675235 56.452485
#> Warning: NaNs produced
#> REFLECTION 212 57.185361 56.267132
#> HI-REDUCTION 214 56.896382 56.267132
#> EXTENSION 216 56.452485 55.396118
#> LO-REDUCTION 218 56.429536 55.260150
#> EXTENSION 220 56.267132 51.721751
#> LO-REDUCTION 222 55.396118 51.721751
#> HI-REDUCTION 224 55.260150 51.721751
#> LO-REDUCTION 226 54.477910 51.721751
#> EXTENSION 228 53.896320 47.475276
#> HI-REDUCTION 230 52.586416 47.475276
#> LO-REDUCTION 232 52.326430 47.475276
#> Warning: NaNs produced
#> HI-REDUCTION 234 51.721751 47.475276
#> EXTENSION 236 50.948154 47.004641
#> Warning: NaNs produced
#> HI-REDUCTION 238 49.353867 47.004641
#> LO-REDUCTION 240 49.073246 47.004641
#> HI-REDUCTION 242 47.760300 47.004641
#> HI-REDUCTION 244 47.612588 47.004641
#> EXTENSION 246 47.475276 46.317208
#> REFLECTION 248 47.262919 45.622102
#> LO-REDUCTION 250 47.004641 45.027214
#> LO-REDUCTION 252 46.317208 44.861974
#> HI-REDUCTION 254 45.622102 44.861974
#> HI-REDUCTION 256 45.329985 44.861974
#> REFLECTION 258 45.088177 44.810057
#> REFLECTION 260 45.027214 44.266724
#> REFLECTION 262 44.861974 44.138604
#> HI-REDUCTION 264 44.810057 44.138604
#> HI-REDUCTION 266 44.427386 44.138604
#> REFLECTION 268 44.337632 44.032394
#> REFLECTION 270 44.266724 43.951003
#> REFLECTION 272 44.138604 43.800632
#> LO-REDUCTION 274 44.032394 43.774492
#> HI-REDUCTION 276 43.951003 43.774492
#> EXTENSION 278 43.840938 43.473799
#> EXTENSION 280 43.800632 43.313788
#> REFLECTION 282 43.774492 43.281572
#> EXTENSION 284 43.473799 42.844823
#> EXTENSION 286 43.313788 42.373266
#> EXTENSION 288 43.281572 42.182610
#> LO-REDUCTION 290 42.844823 42.182610
#> EXTENSION 292 42.373266 40.670656
#> LO-REDUCTION 294 42.207204 40.670656
#> LO-REDUCTION 296 42.182610 40.670656
#> EXTENSION 298 41.638092 39.458445
#> EXTENSION 300 41.153727 36.769684
#> LO-REDUCTION 302 40.670656 36.769684
#> LO-REDUCTION 304 39.458445 36.769684
#> Warning: NaNs produced
#> REFLECTION 306 37.921832 35.200274
#> HI-REDUCTION 308 37.448116 35.200274
#> EXTENSION 310 37.010754 33.039041
#> Warning: NaNs produced
#> REFLECTION 312 36.769684 29.418643
#> Warning: NaNs produced
#> HI-REDUCTION 314 35.200274 29.418643
#> LO-REDUCTION 316 34.772622 29.418643
#> Warning: NaNs produced
#> REFLECTION 318 33.039041 26.451462
#> Warning: NaNs produced
#> REFLECTION 320 32.651520 24.329467
#> Warning: NaNs produced
#> HI-REDUCTION 322 30.273241 24.329467
#> Warning: NaNs produced
#> HI-REDUCTION 324 29.418643 24.329467
#> LO-REDUCTION 326 28.501430 24.208132
#> Warning: NaNs produced
#> HI-REDUCTION 328 26.551550 24.208132
#> Warning: NaNs produced
#> REFLECTION 330 26.451462 19.349720
#> Warning: NaNs produced
#> HI-REDUCTION 332 24.329467 19.349720
#> HI-REDUCTION 334 24.208132 19.349720
#> Warning: NaNs produced
#> REFLECTION 336 24.021515 14.604988
#> Warning: NaNs produced
#> HI-REDUCTION 338 21.734688 14.604988
#> Warning: NaNs produced
#> HI-REDUCTION 340 21.122190 14.604988
#> Warning: NaNs produced
#> HI-REDUCTION 342 20.117199 14.604988
#> Warning: NaNs produced
#> HI-REDUCTION 344 19.469040 14.604988
#> HI-REDUCTION 346 19.349720 14.604988
#> LO-REDUCTION 348 18.821741 14.604988
#> LO-REDUCTION 350 18.286990 14.604988
#> LO-REDUCTION 352 18.228687 14.604988
#> Warning: NaNs produced
#> HI-REDUCTION 354 16.729009 14.604988
#> Warning: NaNs produced
#> REFLECTION 356 15.451851 13.780624
#> Warning: NaNs produced
#> REFLECTION 358 14.672805 11.868968
#> HI-REDUCTION 360 14.604988 11.868968
#> Warning: NaNs produced
#> HI-REDUCTION 362 13.780624 11.868968
#> LO-REDUCTION 364 13.604789 11.868968
#> EXTENSION 366 13.377487 10.876970
#> LO-REDUCTION 368 13.143379 10.807862
#> Warning: NaNs produced
#> HI-REDUCTION 370 12.008277 10.807862
#> HI-REDUCTION 372 11.868968 10.807862
#> LO-REDUCTION 374 11.419716 10.807862
#> REFLECTION 376 10.876970 10.432530
#> REFLECTION 378 10.836609 10.333558
#> LO-REDUCTION 380 10.807862 10.275494
#> REFLECTION 382 10.432530 10.076943
#> LO-REDUCTION 384 10.333558 10.076943
#> LO-REDUCTION 386 10.275494 10.007425
#> REFLECTION 388 10.081922 9.871004
#> HI-REDUCTION 390 10.076943 9.871004
#> REFLECTION 392 10.007425 9.832550
#> EXTENSION 394 9.906016 9.608536
#> EXTENSION 396 9.871004 9.477899
#> REFLECTION 398 9.832550 9.431202
#> REFLECTION 400 9.608536 9.391317
#> EXTENSION 402 9.477899 9.064771
#> LO-REDUCTION 404 9.431202 9.064771
#> LO-REDUCTION 406 9.391317 9.064771
#> EXTENSION 408 9.208730 8.588939
#> EXTENSION 410 9.081577 8.388029
#> LO-REDUCTION 412 9.064771 8.388029
#> REFLECTION 414 8.588939 8.109063
#> LO-REDUCTION 416 8.432654 8.109063
#> HI-REDUCTION 418 8.388029 8.109063
#> REFLECTION 420 8.241052 8.094280
#> LO-REDUCTION 422 8.165604 8.080601
#> HI-REDUCTION 424 8.109063 8.080601
#> REFLECTION 426 8.094280 8.069875
#> HI-REDUCTION 428 8.093345 8.069875
#> HI-REDUCTION 430 8.080601 8.069875
#> Exiting from Nelder Mead minimizer
#> 432 function evaluations used
sr5.nls <- nls(sr5)
# NS Herring stock-recruitment dataset
data(nsher)
# already fitted with a Ricker SR model
summary(nsher)
#> An object of class "FLSR"
#>
#> Name:
#> Description:
#> Quant: age
#> Dims: age year unit season area iter
#> 1 45 1 1 1 1
#>
#> Range: min minyear max maxyear
#> 0 1960 0 2004
#>
#>
#> Model: rec ~ a * ssb * exp(-b * ssb)
#> An object of class "FLPar"
#> params
#> a b
#> 1.19e+02 9.45e-03
#> units: NA
#> Log-likelihood: 15.862(0)
#> Variance-covariance:
#> a b
#> a 255.3388181 1.808870e-02
#> b 0.0180887 1.992659e-06
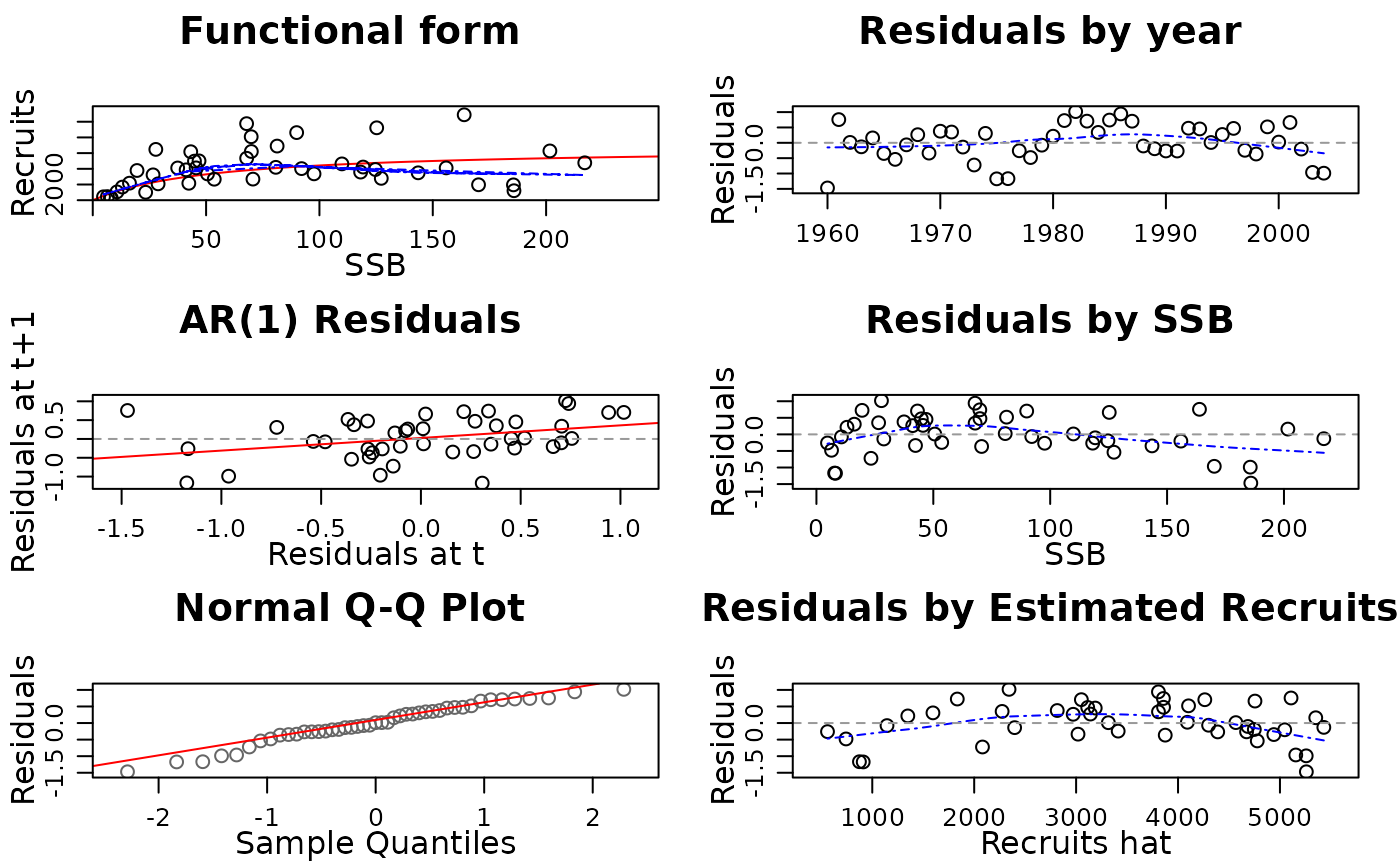
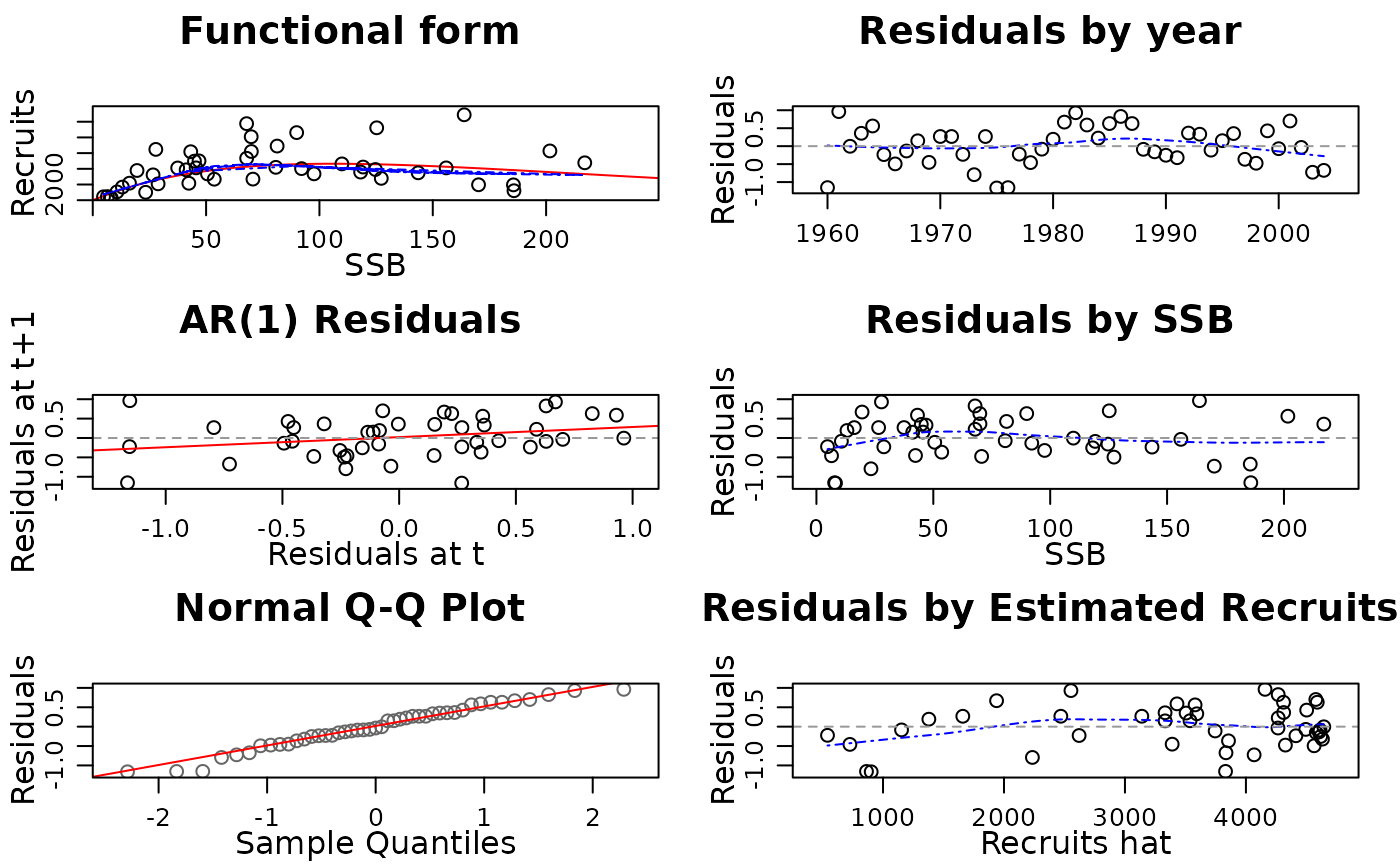
plot(nsher)
# change model
model(nsher) <- bevholt()
# fit through MLE
nsher <- fmle(nsher)
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -10.336211
#> Scaled convergence tolerance is 1.54022e-07
#> Stepsize computed as 501.110000
#> BUILD 3 44.842344 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 5 31.685209 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 7 17.913114 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 9 5.415279 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 11 -3.412974 -11.603908
#> HI-REDUCTION 13 -8.018030 -11.603908
#> LO-REDUCTION 15 -10.336211 -11.603908
#> LO-REDUCTION 17 -11.081040 -11.603908
#> EXTENSION 19 -11.295930 -12.061705
#> LO-REDUCTION 21 -11.603908 -12.061705
#> REFLECTION 23 -11.813826 -12.087620
#> REFLECTION 25 -12.061705 -12.199591
#> LO-REDUCTION 27 -12.087620 -12.199591
#> LO-REDUCTION 29 -12.158184 -12.199591
#> LO-REDUCTION 31 -12.191726 -12.199591
#> HI-REDUCTION 33 -12.192269 -12.199591
#> HI-REDUCTION 35 -12.197784 -12.199591
#> LO-REDUCTION 37 -12.198015 -12.199591
#> HI-REDUCTION 39 -12.199555 -12.199776
#> REFLECTION 41 -12.199591 -12.200058
#> HI-REDUCTION 43 -12.199776 -12.200092
#> HI-REDUCTION 45 -12.200058 -12.200142
#> HI-REDUCTION 47 -12.200092 -12.200155
#> HI-REDUCTION 49 -12.200142 -12.200160
#> HI-REDUCTION 51 -12.200155 -12.200177
#> HI-REDUCTION 53 -12.200160 -12.200177
#> LO-REDUCTION 55 -12.200171 -12.200179
#> HI-REDUCTION 57 -12.200177 -12.200179
#> HI-REDUCTION 59 -12.200178 -12.200179
#> HI-REDUCTION 61 -12.200179 -12.200179
#> HI-REDUCTION 63 -12.200179 -12.200179
#> HI-REDUCTION 65 -12.200179 -12.200179
#> Exiting from Nelder Mead minimizer
#> 67 function evaluations used
plot(nsher)
