New basic plot methods for some FLR classes are defined in ggplotFL.
# S4 method for FLQuant,missing
plot(x, probs = c(0.05, 0.25, 0.5, 0.75, 0.95), na.rm = FALSE, ...)
# S4 method for FLQuant,FLQuant
plot(
x,
y,
...,
probs = c(0.05, 0.25, 0.5, 0.75, 0.95),
na.rm = FALSE,
iter = NULL
)
# S4 method for FLQuants,missing
plot(
x,
probs = c(0.05, 0.25, 0.5, 0.75, 0.95),
na.rm = FALSE,
worm = iter,
iter = NULL
)
# S4 method for FLQuants,FLPar
plot(x, y, ...)
# S4 method for FLQuants,FLPars
plot(x, y, ...)
# S4 method for FLQuantPoint,missing
plot(x, mean = TRUE, median = TRUE)
# S4 method for FLQuantPoint,FLQuant
plot(x, y, na.rm = FALSE, ...)
# S4 method for FLQuantPoint,FLQuants
plot(x, y, na.rm = FALSE, mean = TRUE, median = TRUE, ...)
# S4 method for FLPar,missing
plot(x, names = NULL)
# S4 method for FLStock,missing
plot(
x,
metrics = list(Rec = rec, SSB = ssb, Catch = catch, F = fbar),
na.rm = TRUE,
...
)
# S4 method for FLStock,FLStock
plot(
x,
y,
metrics = list(Rec = rec, SSB = ssb, Catch = catch, F = fbar),
probs = c(0.1, 0.33, 0.5, 0.66, 0.9),
na.rm = TRUE,
iter = NULL,
...
)
# S4 method for FLStock,FLPar
plot(x, y, metrics = list(Rec = rec, SSB = ssb, Catch = catch, F = fbar), ...)
# S4 method for FLStocks,missing
plot(
x,
metrics = list(Rec = function(x) unitSums(rec(x)), SB = function(x) unitSums(ssb(x)), C
= function(x) unitSums(catch(x)), F = function(x) unitMeans(fbar(x))),
probs = c(0.1, 0.33, 0.5, 0.66, 0.9),
alpha = c(0.1, 0.4),
worm = iter,
iter = NULL,
...
)
# S4 method for FLStocks,missing
plot(
x,
metrics = list(Rec = function(x) unitSums(rec(x)), SB = function(x) unitSums(ssb(x)), C
= function(x) unitSums(catch(x)), F = function(x) unitMeans(fbar(x))),
probs = c(0.1, 0.33, 0.5, 0.66, 0.9),
alpha = c(0.1, 0.4),
worm = iter,
iter = NULL,
...
)
# S4 method for FLStocks,FLPar
plot(
x,
y,
na.rm = TRUE,
metrics = function(x, y) FLQuants(SSB = ssb(x)/y[, "ssb", ], F = fbar(x)/y[, "harvest",
], Catch = catch(x))
)
# S4 method for FLStock,FLStocks
plot(x, y, ...)
# S4 method for FLSR,missing
plot(x, y, ...)
# S4 method for FLSRs,ANY
plot(x, legend_label = names(x), facets = FALSE, ...)
# S4 method for FLBiol,missing
plot(x, metrics = list(Rec = function(x) n(x)[1, ], B = tsb), ...)
# S4 method for FLBiols,missing
plot(x, metrics = list(Rec = function(x) n(x)[1, ], B = tsb), ...)
# S4 method for FLIndexBiomass,missing
plot(x, y, ...)
# S4 method for FLIndex,missing
plot(x)
# S4 method for FLIndices,missing
plot(x)Arguments
- x
FLR object to plot
- probs
Quantiles to calculate along the iter dimension. A vector of length 5, for the lower outer, lower inner, central, upper inner and upper outer quantiles. Defaults to the 66 and 80 percent quantiles, plus median line.
- na.rm
Should NAs be deleted in quantile calculations?, defaults to TRUE.
- ...
Other arguments to be passed to the corresponding ggplot call.
- y
FLR object to plot
- iter
Individual iterations to show as worm plots over the quantiles.
- worm
Individual iterations to show as worm plots over the quantiles.
- metrics
function returning an FLQuants for each FLStock
- alpha
alpha values for the quantile ribbons, defaults to 0.10 and 0.40.
- legend_label
function to create the legend labels
Details
The coertion to *data.frame* that is carried out in the plot methods sets the argument `date=TRUE`. This generates a new column of class `POSIXct` for the first day of the first month of each season. If the `season` dimension of the object being plotted is of length greater than one, `date` will be used as variable on the x axis of the plot. Otherwise, it will be `year`. Keep this in mind when adding extra elements to the plot (see examples below).
A similar mechanism is used for the *y* axis, depending on the length of the `iter` dimension. For objects with no *iters*, a single line is plotted for each *FLQuant*, and the *y* axis is mapped to the `data` column of the *data.frame*. For objects with iterations, i.e. with length greater than 1 on the `iter` dimension, the default plots show the quantiles of the distribution and the *y* axis is mapped to the middle quantile, by default `50 examples below on how to refer to these variables when adding elements to the plot.
See also
ISOdate ggplot
Examples
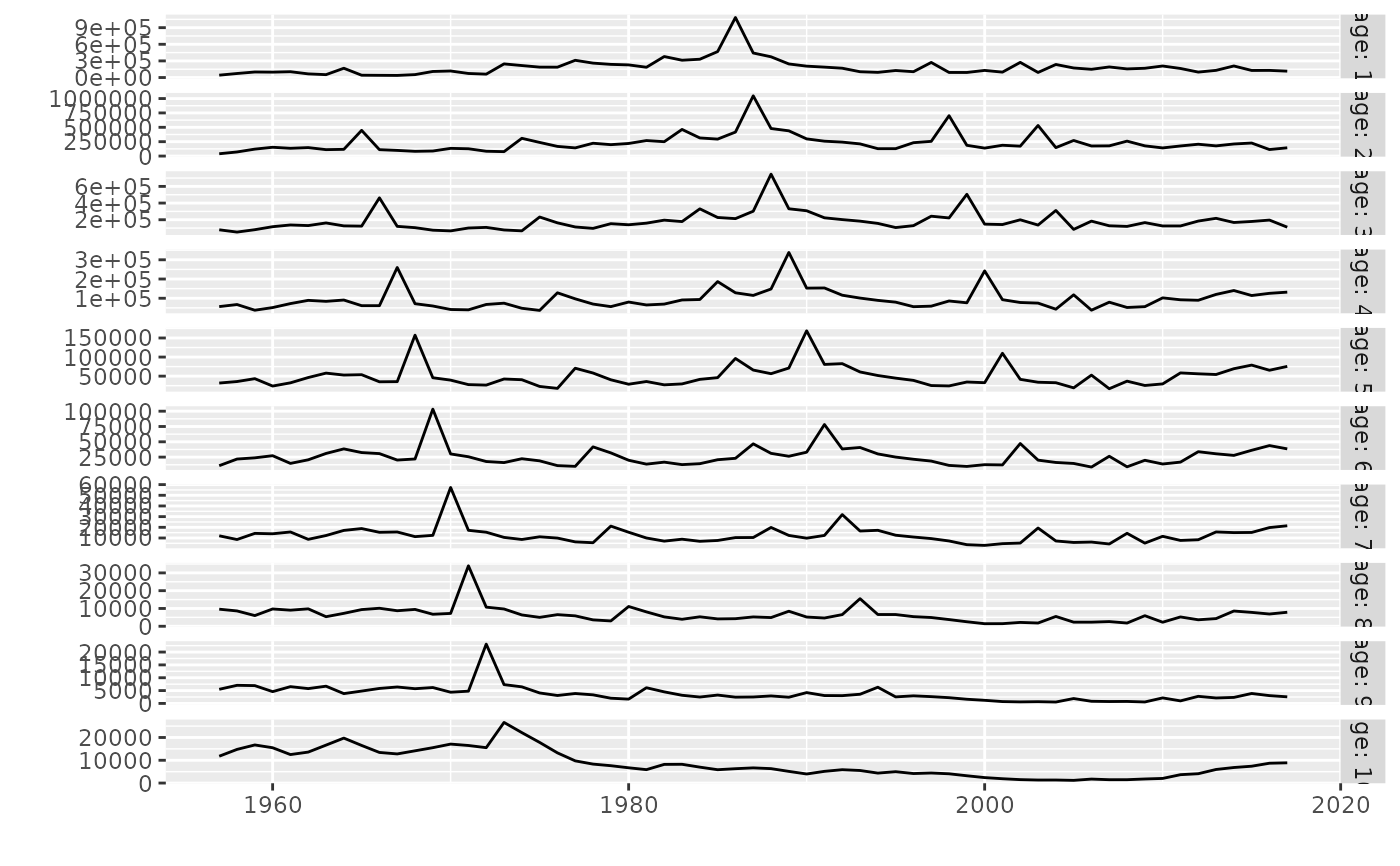
# Plot a single FLQuant
data(ple4)
plot(catch.n(ple4))
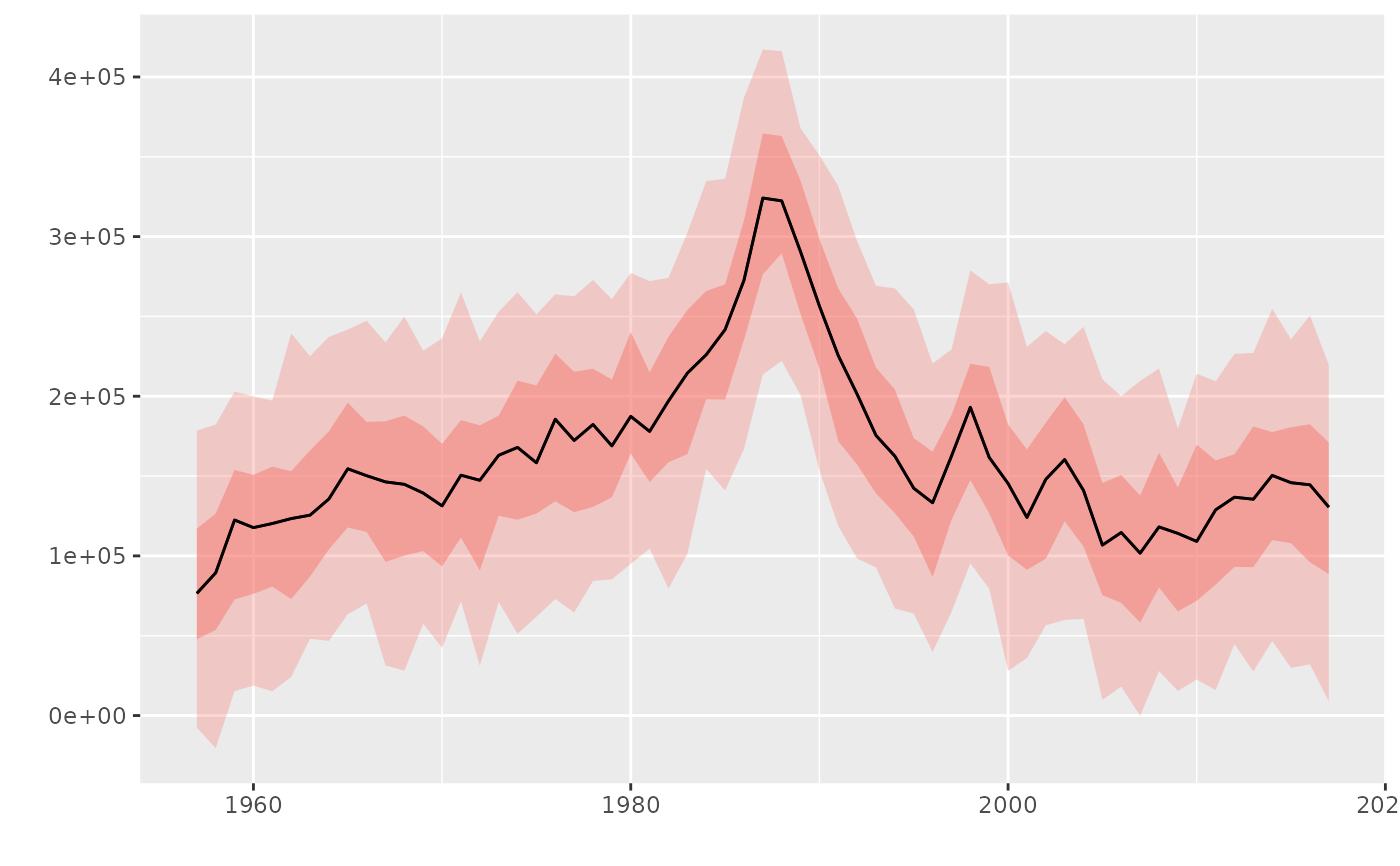
 # Plot an FLQuant with iters, shows quantiles
flq <- rnorm(100, catch(ple4), 60000)
plot(flq)
# Plot an FLQuant with iters, shows quantiles
flq <- rnorm(100, catch(ple4), 60000)
plot(flq)
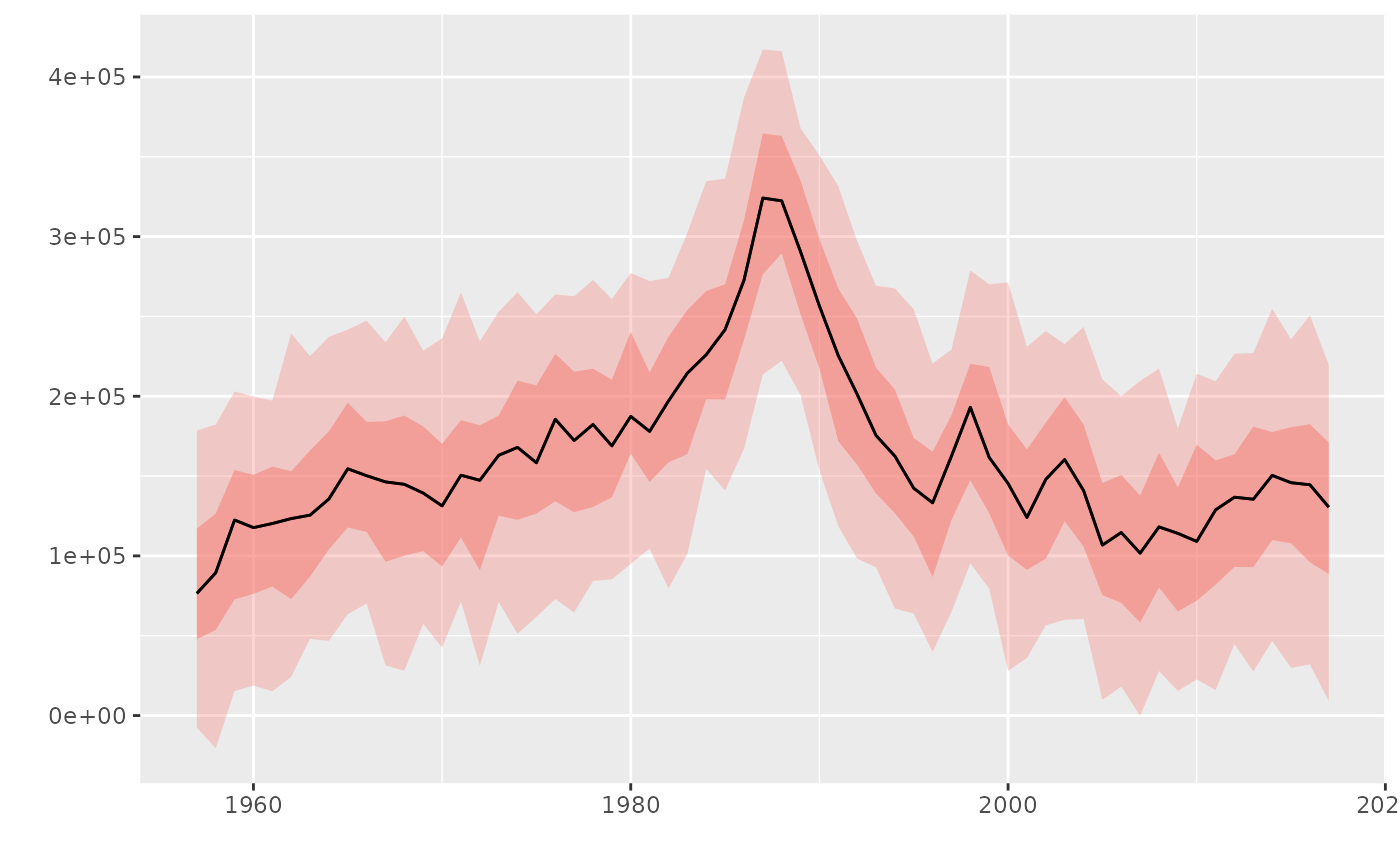
 # Specify quantiles, default is c(0.10, 0.33, 0.50, 0.66, 0.90)
plot(flq, probs=c(0.05, 0.25, 0.50, 0.75, 0.95))
# Specify quantiles, default is c(0.10, 0.33, 0.50, 0.66, 0.90)
plot(flq, probs=c(0.05, 0.25, 0.50, 0.75, 0.95))
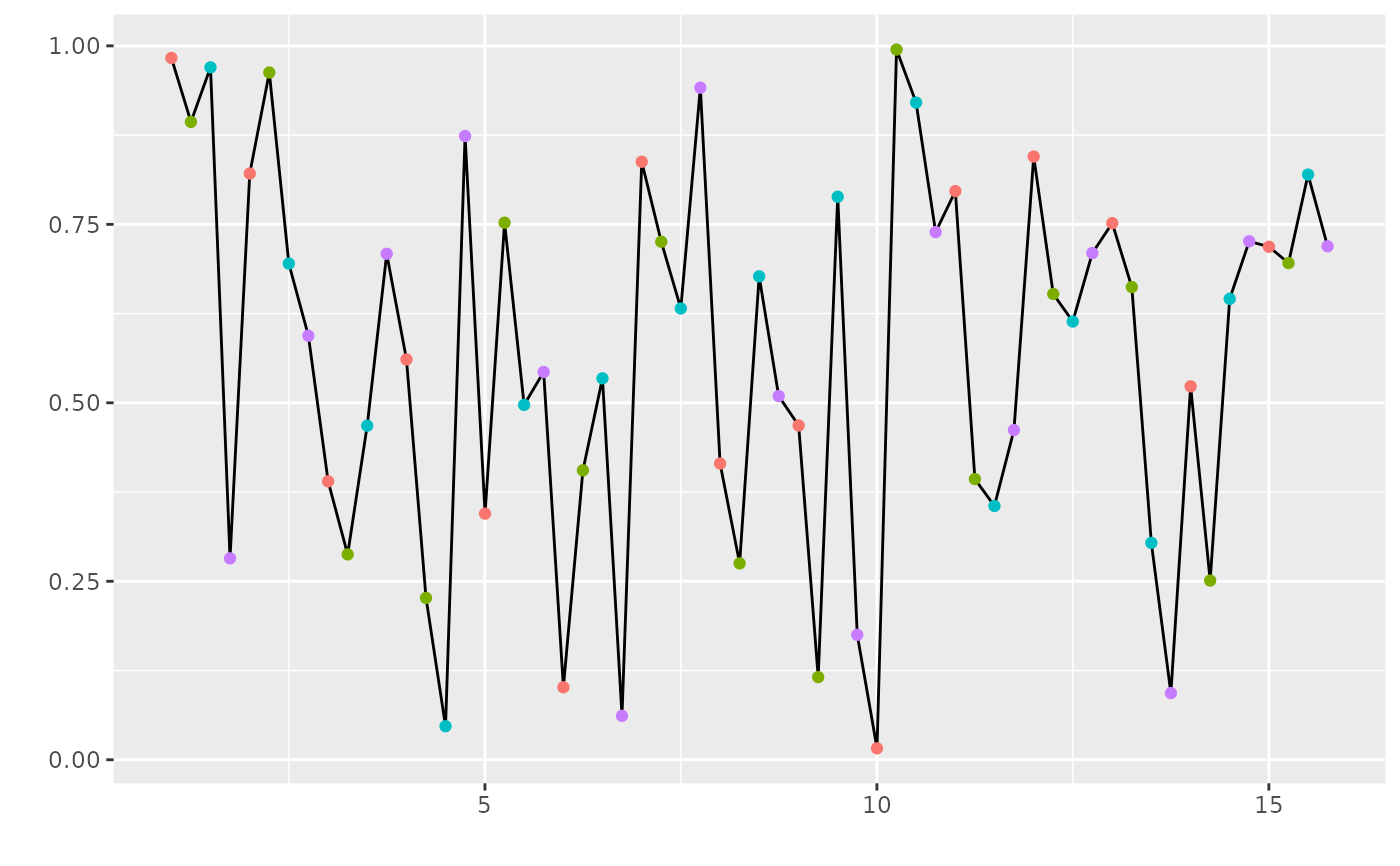
 # Adding extra elements to an FLQuant plot, with seasons
flq <- FLQuant(runif(200), dim=c(1,15,1,4))
plot(flq) + geom_point(aes(x=date, y=data, colour=season))
# Adding extra elements to an FLQuant plot, with seasons
flq <- FLQuant(runif(200), dim=c(1,15,1,4))
plot(flq) + geom_point(aes(x=date, y=data, colour=season))
 # or without them
flq <- FLQuant(runif(200), dim=c(1,15))
plot(flq) + geom_point(aes(x=year, y=data))
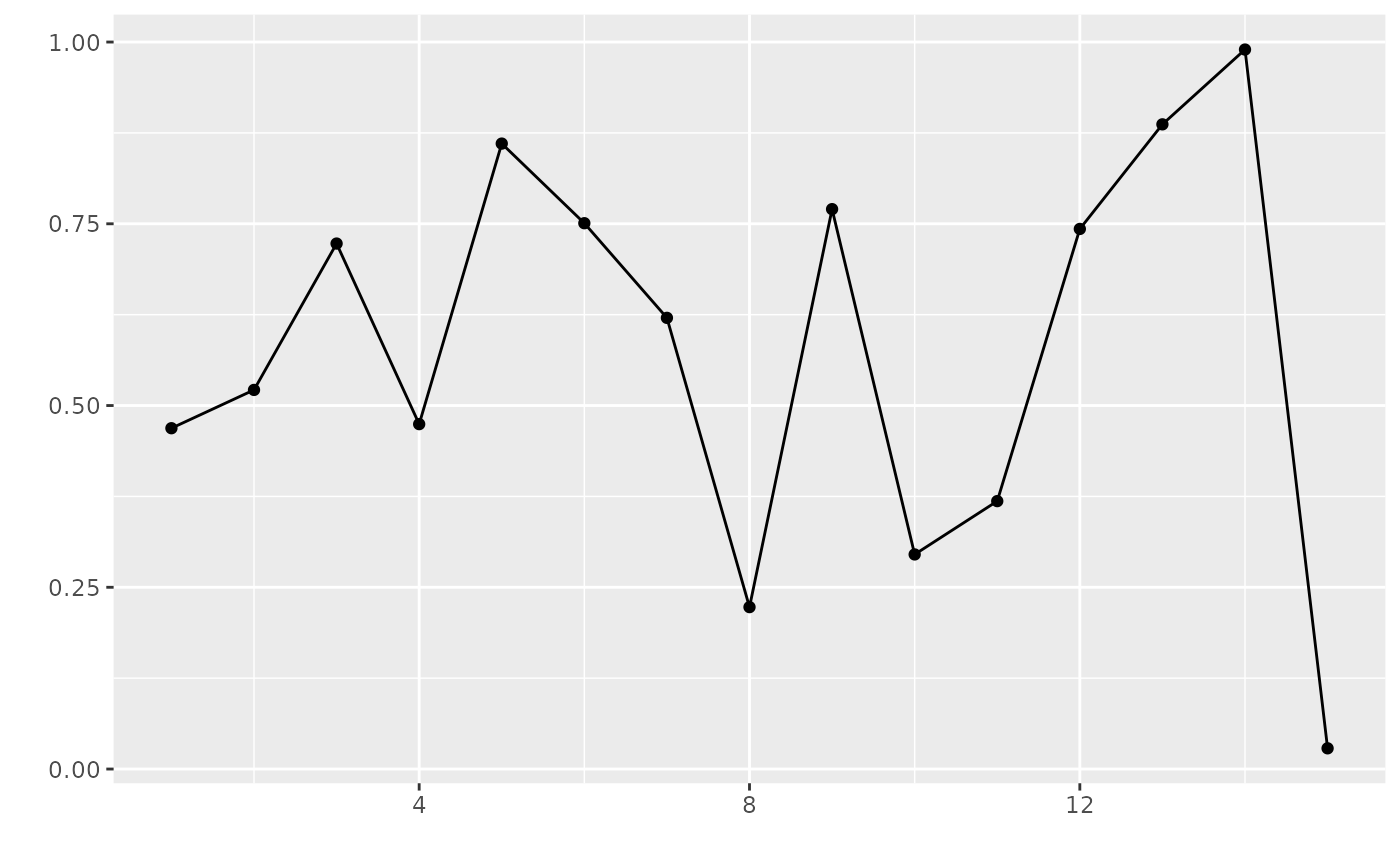
# or without them
flq <- FLQuant(runif(200), dim=c(1,15))
plot(flq) + geom_point(aes(x=year, y=data))
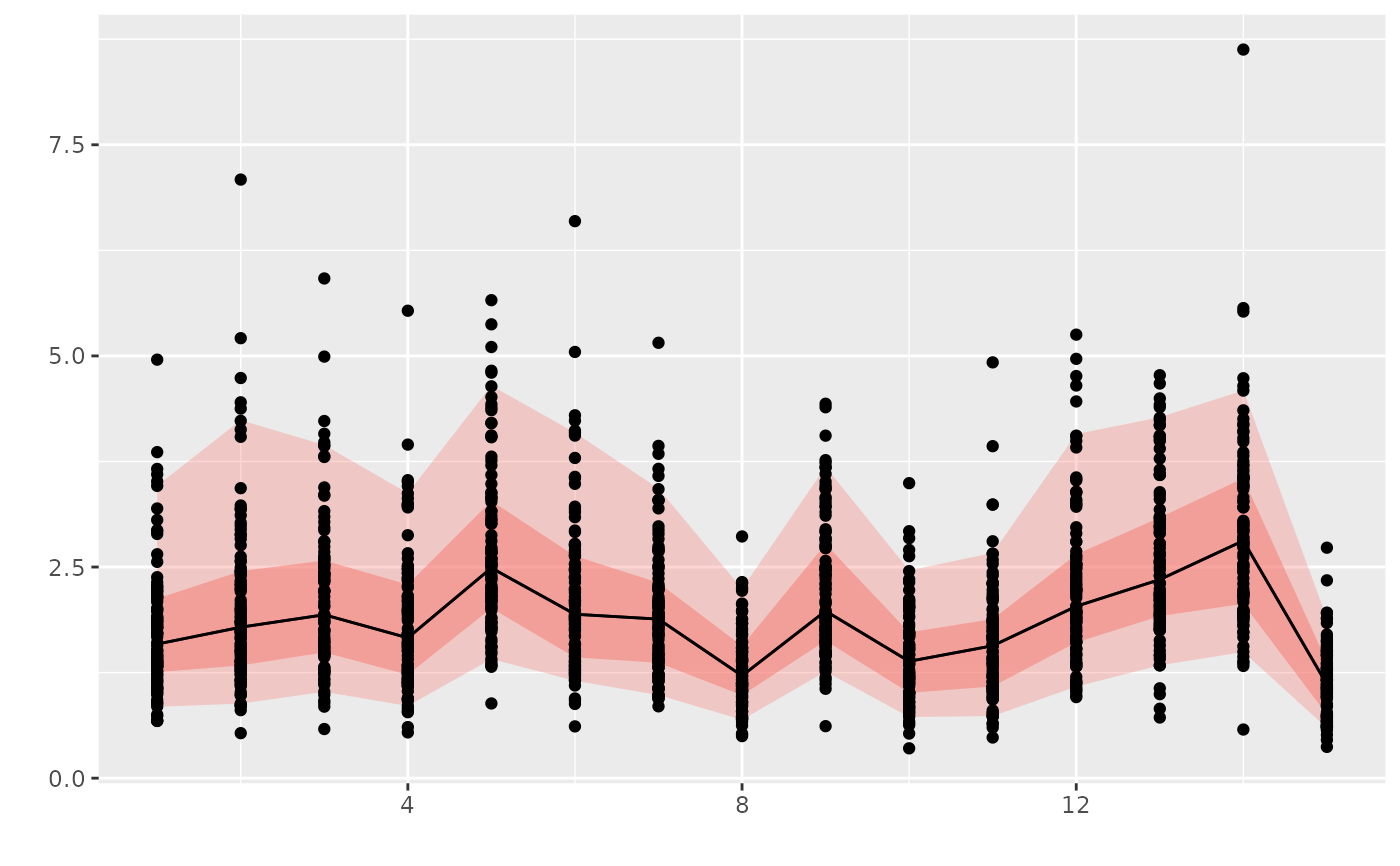
 # For an object with iter
flq <- rlnorm(100, flq, 0.4)
plot(flq) + geom_point(aes(x=year, y=data))
# For an object with iter
flq <- rlnorm(100, flq, 0.4)
plot(flq) + geom_point(aes(x=year, y=data))
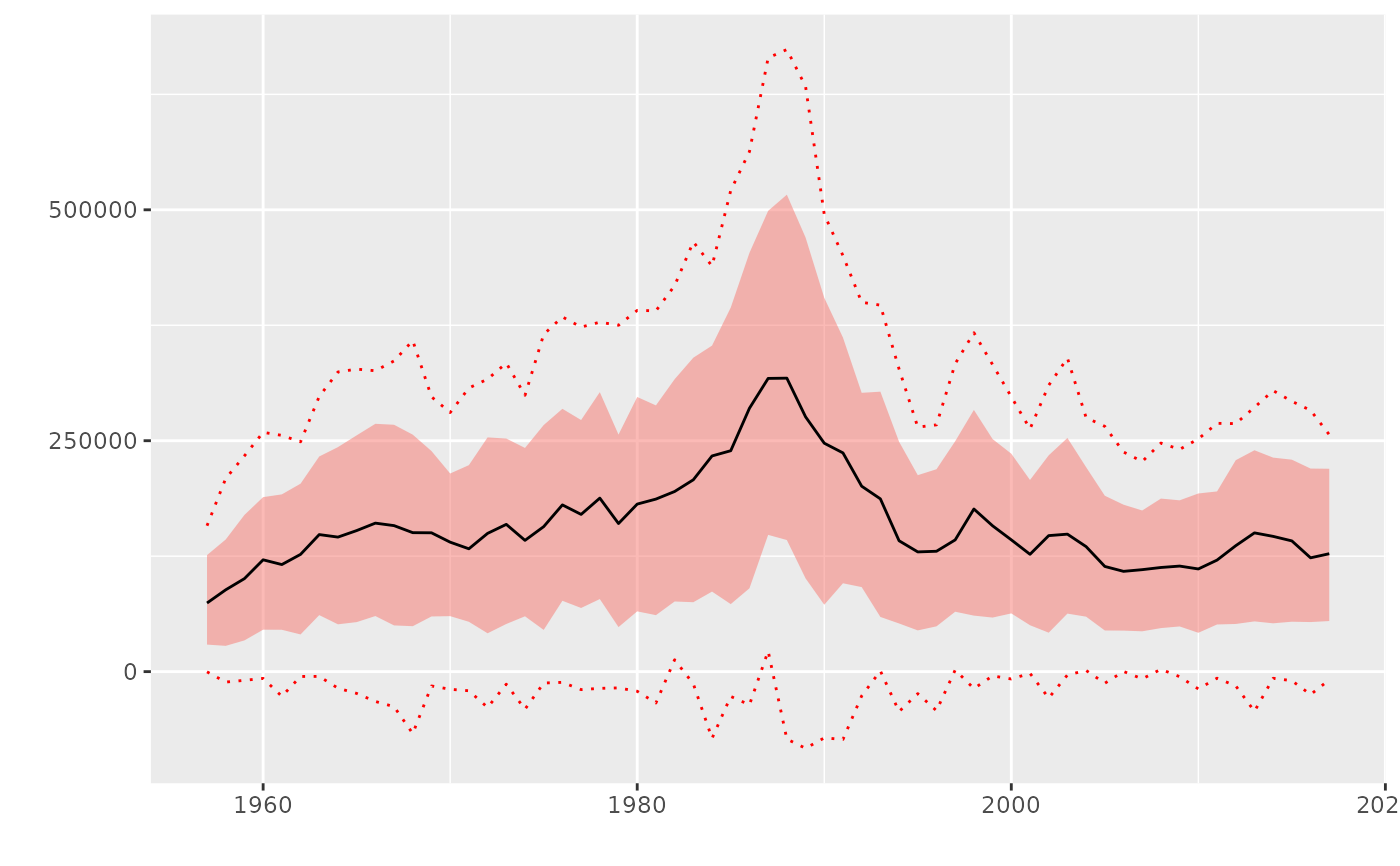
 # To plot(FLQuant) as in previous versions of ggplotFL
plot(rnorm(300, catch(ple4), catch(ple4)/2), probs=c(0.10, 0.5, 0.90)) +
geom_flquantiles(probs=c(0.01), linetype=3, colour="red", alpha=0.1) +
geom_flquantiles(probs=c(0.99), linetype=3, colour="red", alpha=0.1)
# To plot(FLQuant) as in previous versions of ggplotFL
plot(rnorm(300, catch(ple4), catch(ple4)/2), probs=c(0.10, 0.5, 0.90)) +
geom_flquantiles(probs=c(0.01), linetype=3, colour="red", alpha=0.1) +
geom_flquantiles(probs=c(0.99), linetype=3, colour="red", alpha=0.1)
 # plot(FLQuant, FLQuant, ...) to place in one facet
plot(catch(ple4), landings(ple4))
# plot(FLQuant, FLQuant, ...) to place in one facet
plot(catch(ple4), landings(ple4))
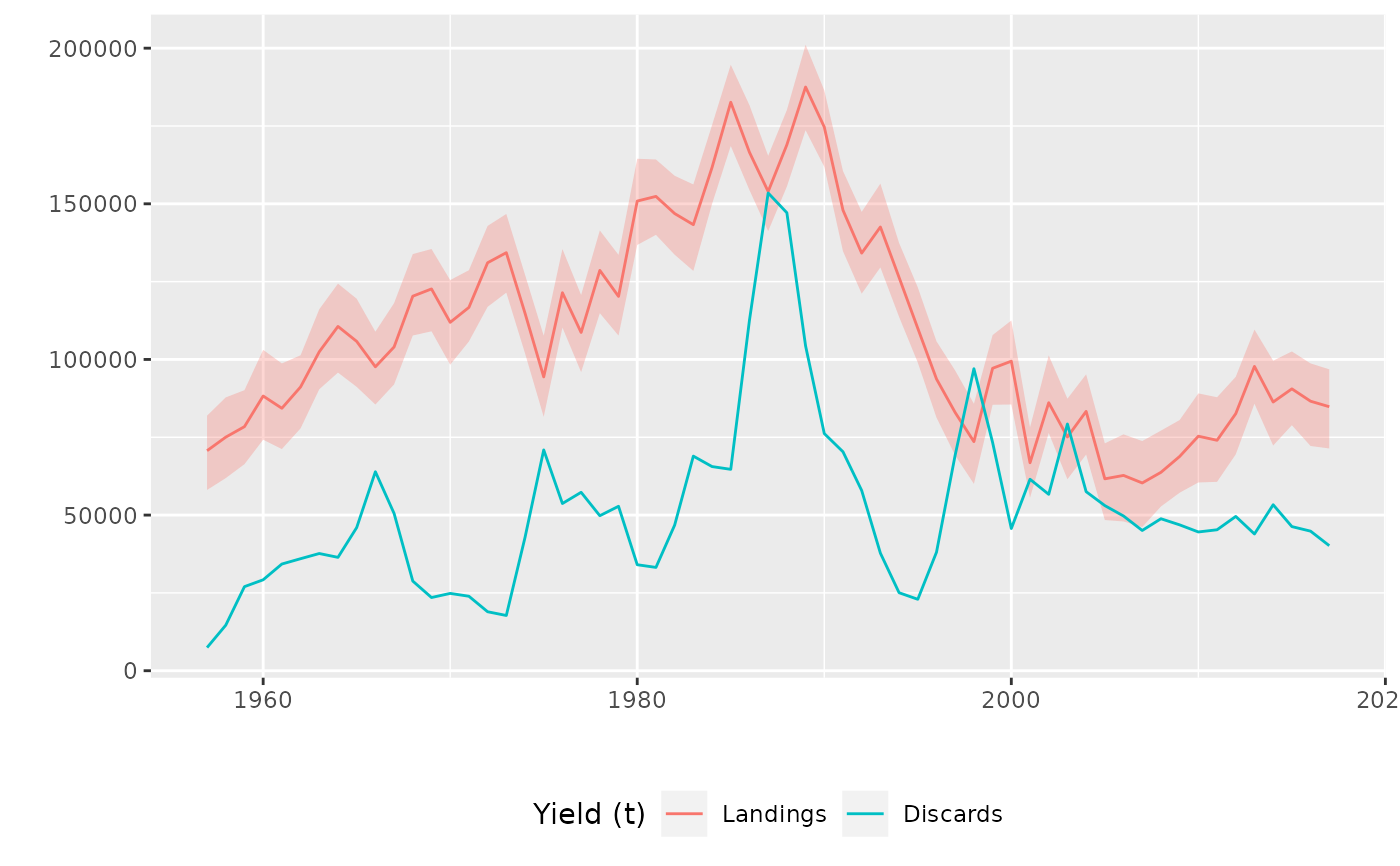
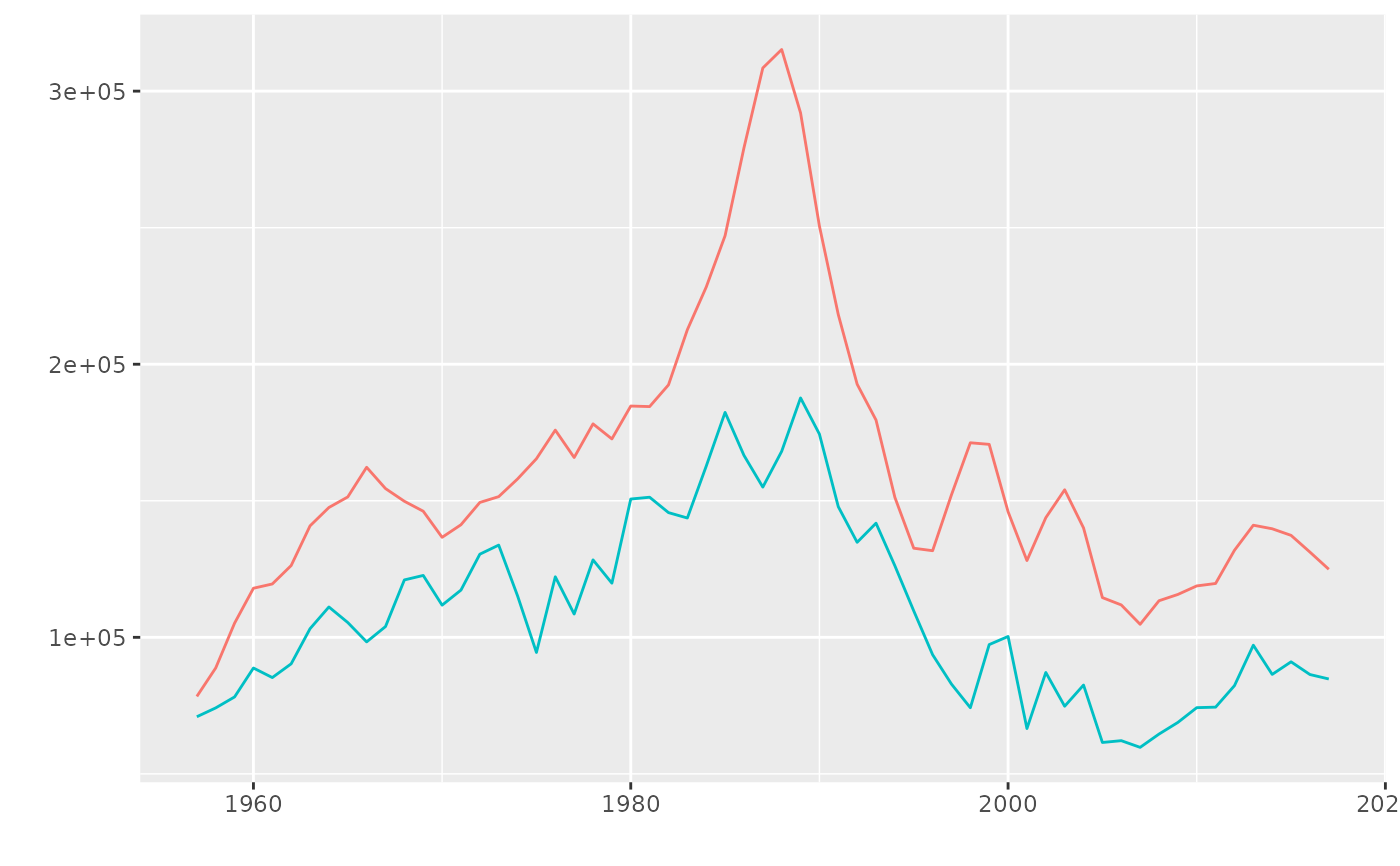 # Add legend by hand
plot(rnorm(200, landings(ple4), 8000), discards(ple4)) +
scale_colour_discrete(name="Yield (t)", labels=c("Landings", "Discards")) +
theme(legend.position="bottom")
# Add legend by hand
plot(rnorm(200, landings(ple4), 8000), discards(ple4)) +
scale_colour_discrete(name="Yield (t)", labels=c("Landings", "Discards")) +
theme(legend.position="bottom")
 # Plot an FLQuants created from ple4 FLStock
data(ple4)
plot(FLQuants(SSB=ssb(ple4), rec=rec(ple4)))
# Plot an FLQuants created from ple4 FLStock
data(ple4)
plot(FLQuants(SSB=ssb(ple4), rec=rec(ple4)))
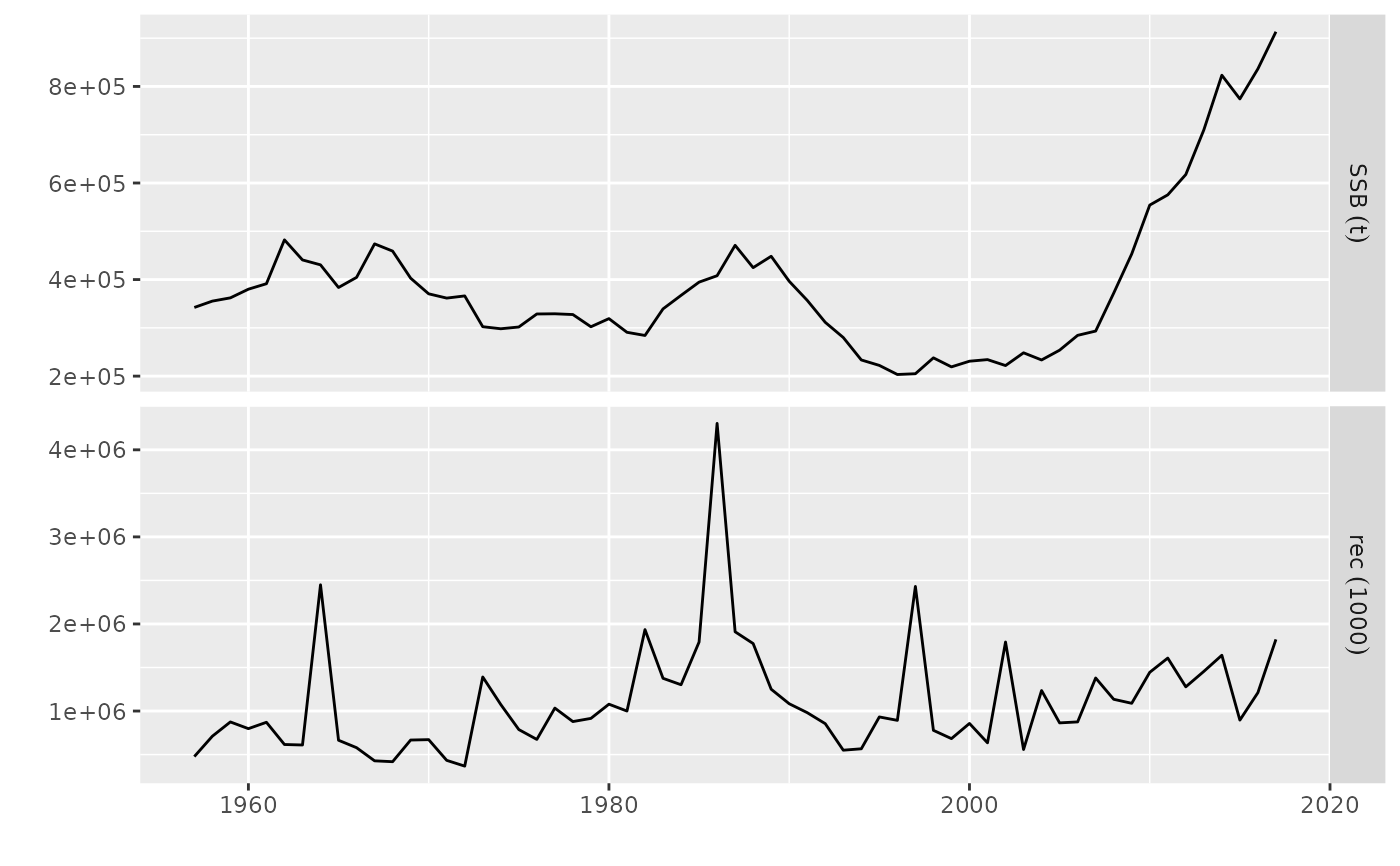 plot(FLQuants(SSB=ssb(ple4), rec=rec(ple4)), probs = NULL)
plot(FLQuants(SSB=ssb(ple4), rec=rec(ple4)), probs = NULL)
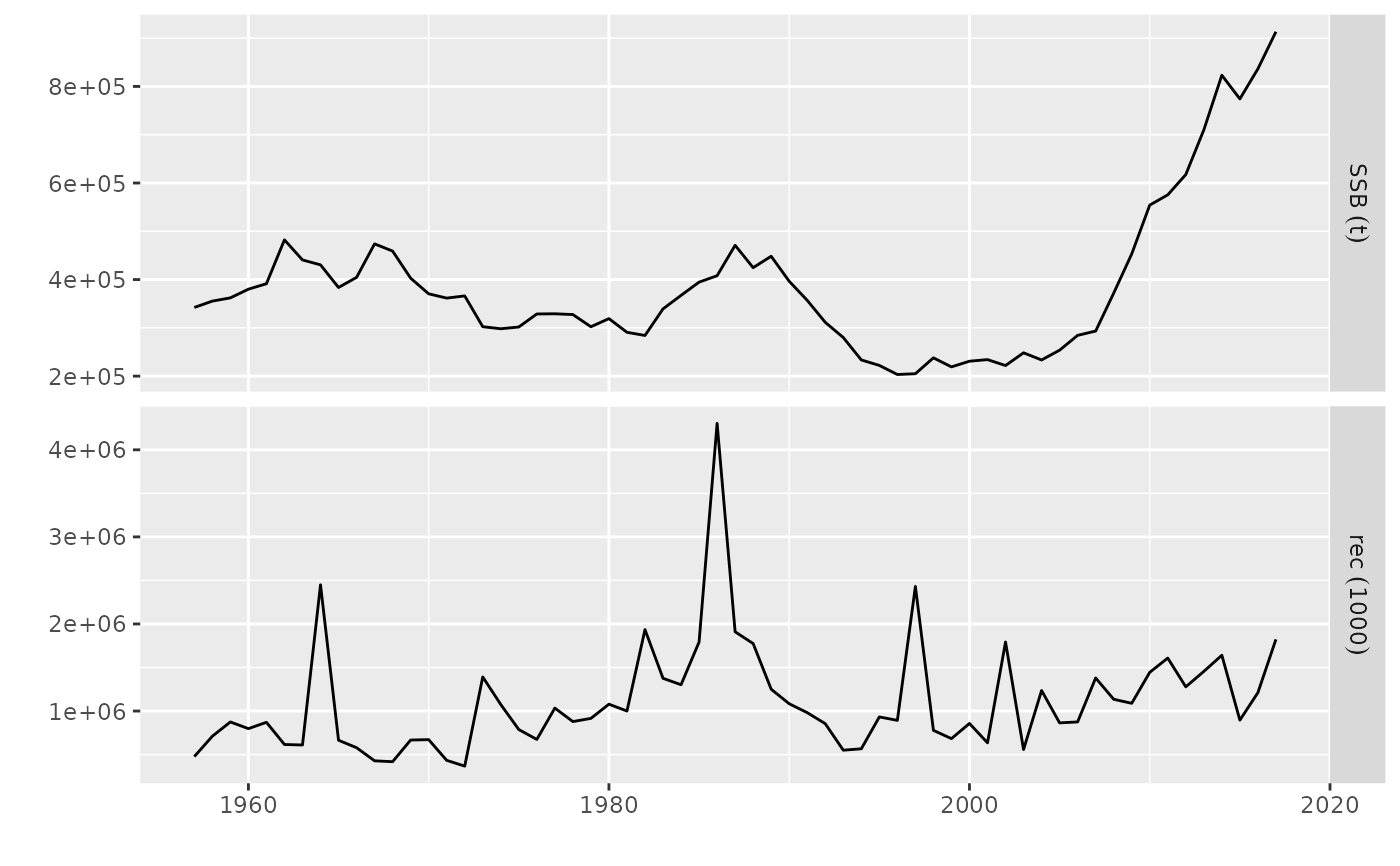 # plot for FLQuants, FLPar
data(ple4)
rps <- FLPar(F=0.14, Catch=1.29e5, Rec=9.38e5, SSB=1.8e5)
fqs <- metrics(ple4)
plot(fqs, rps)
# plot for FLQuants, FLPar
data(ple4)
rps <- FLPar(F=0.14, Catch=1.29e5, Rec=9.38e5, SSB=1.8e5)
fqs <- metrics(ple4)
plot(fqs, rps)
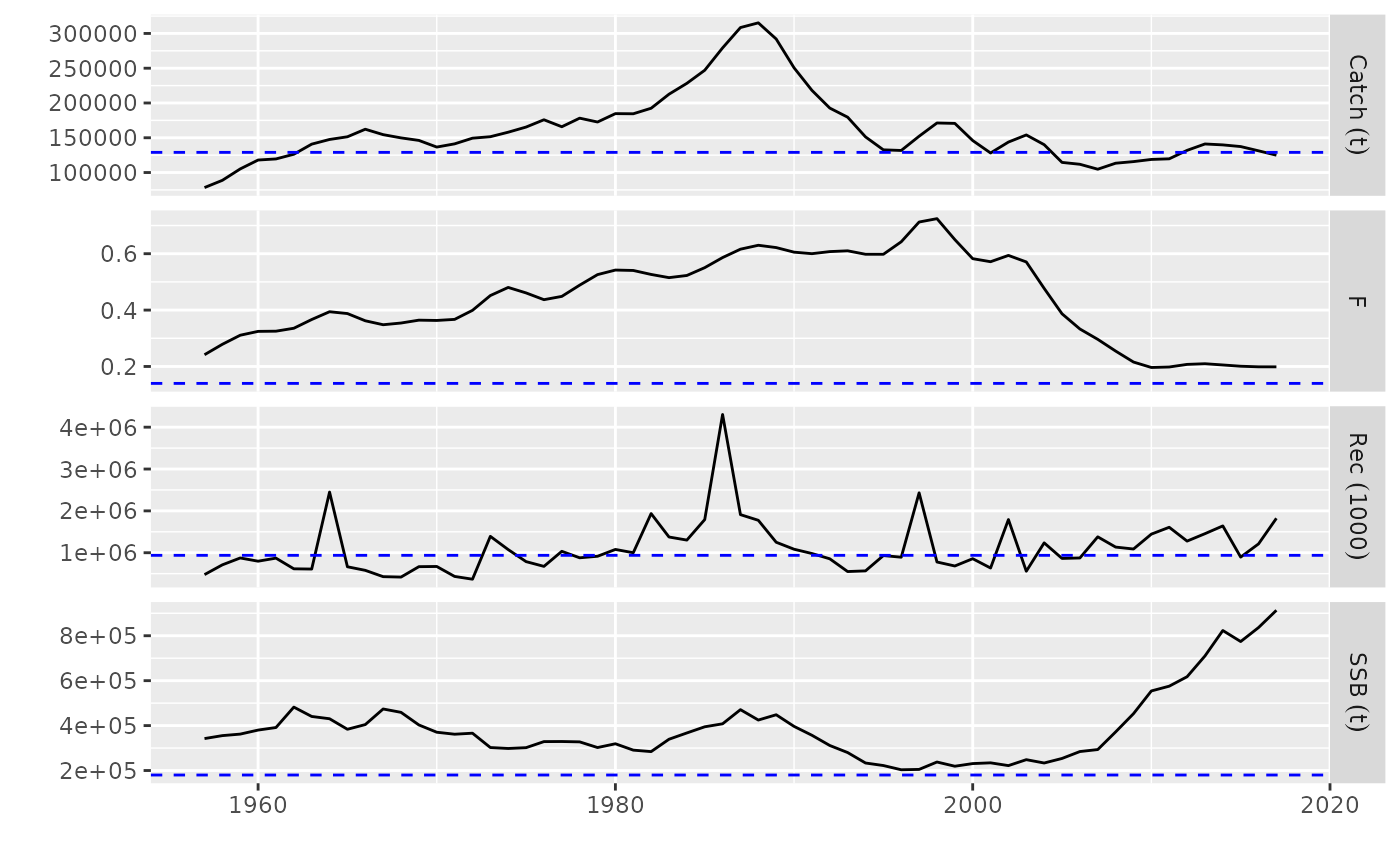 # Works also if reptsa are given for some panels
rps <- FLPar(F=0.14, Catch=1.29e5, SSB=1.8e5)
plot(fqs, rps)
# Works also if reptsa are given for some panels
rps <- FLPar(F=0.14, Catch=1.29e5, SSB=1.8e5)
plot(fqs, rps)
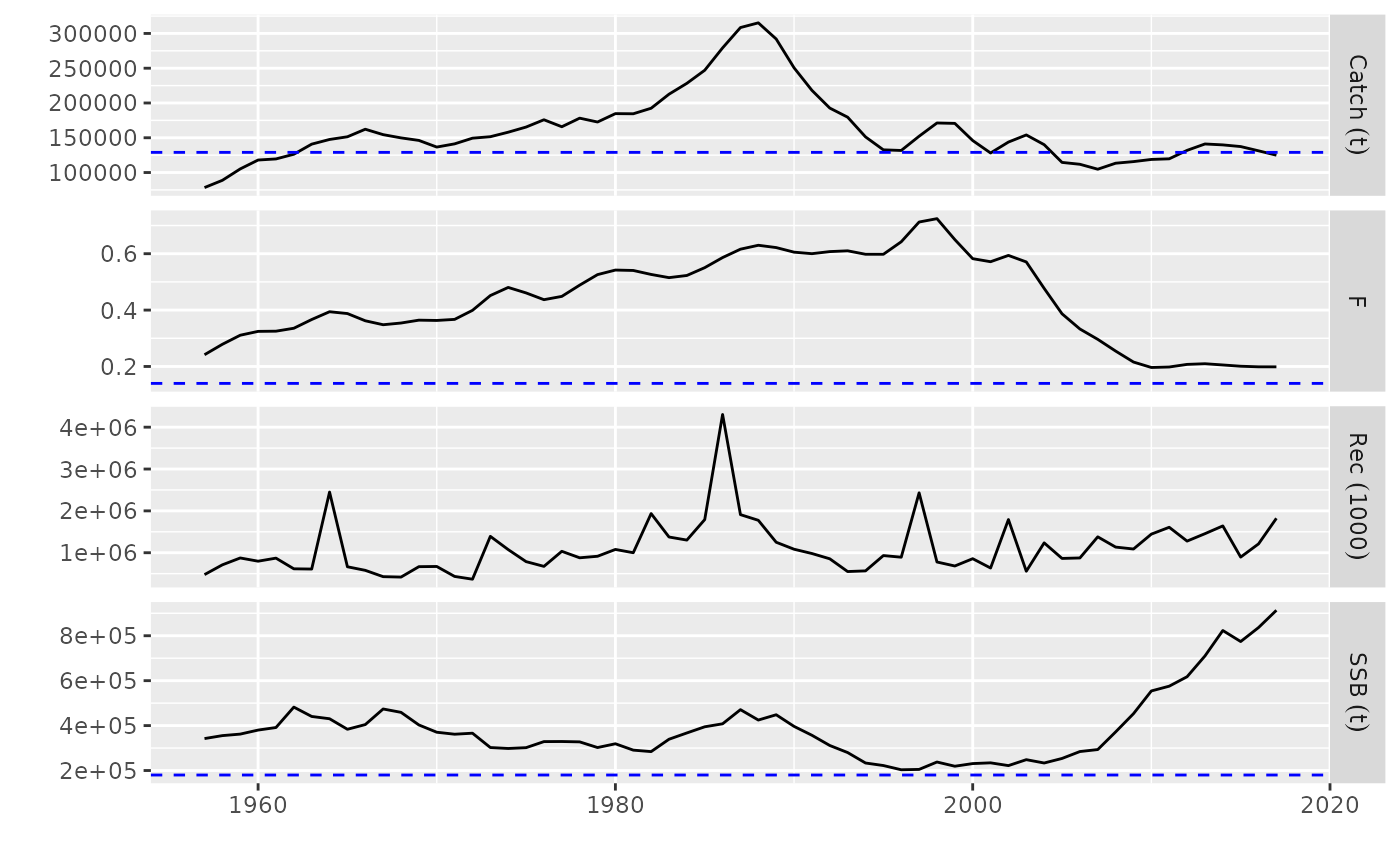 # plot for FLQuants, FLPars
data(ple4)
rps <- FLPars(F=FLPar(Fmsy=0.14, Fpa=0.35), SSB=FLPar(SBmsy=1.8e5, SBlim=1.1e5))
fqs <- metrics(ple4, list(SSB=ssb, F=fbar))
plot(fqs, rps) + ylim(c(0, NA))
# plot for FLQuants, FLPars
data(ple4)
rps <- FLPars(F=FLPar(Fmsy=0.14, Fpa=0.35), SSB=FLPar(SBmsy=1.8e5, SBlim=1.1e5))
fqs <- metrics(ple4, list(SSB=ssb, F=fbar))
plot(fqs, rps) + ylim(c(0, NA))
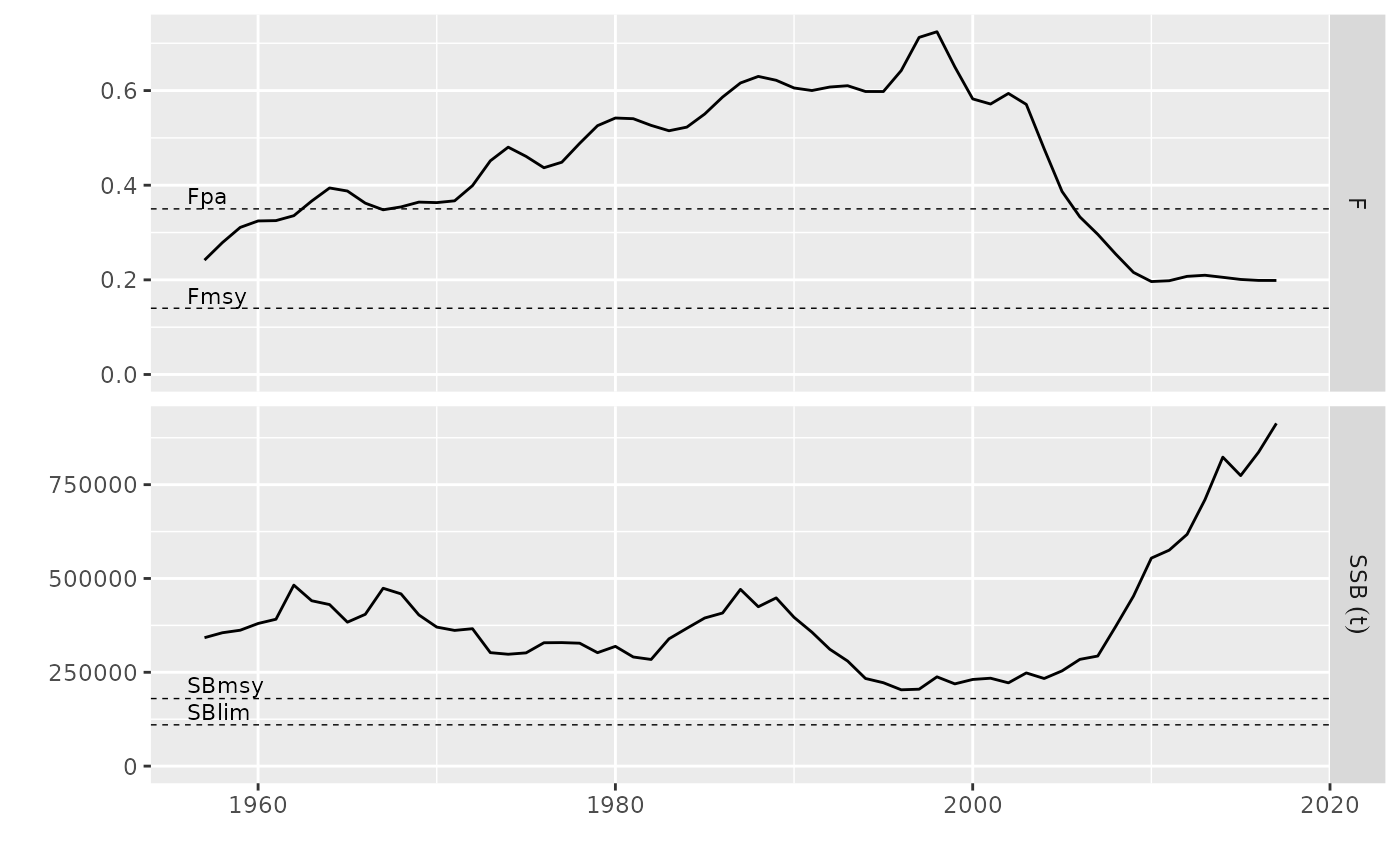 # plot for FLQuantPoint
fqp <- FLQuantPoint(rlnorm(300, log(catch(ple4)), 0.20))
plot(fqp)
# plot for FLQuantPoint
fqp <- FLQuantPoint(rlnorm(300, log(catch(ple4)), 0.20))
plot(fqp)
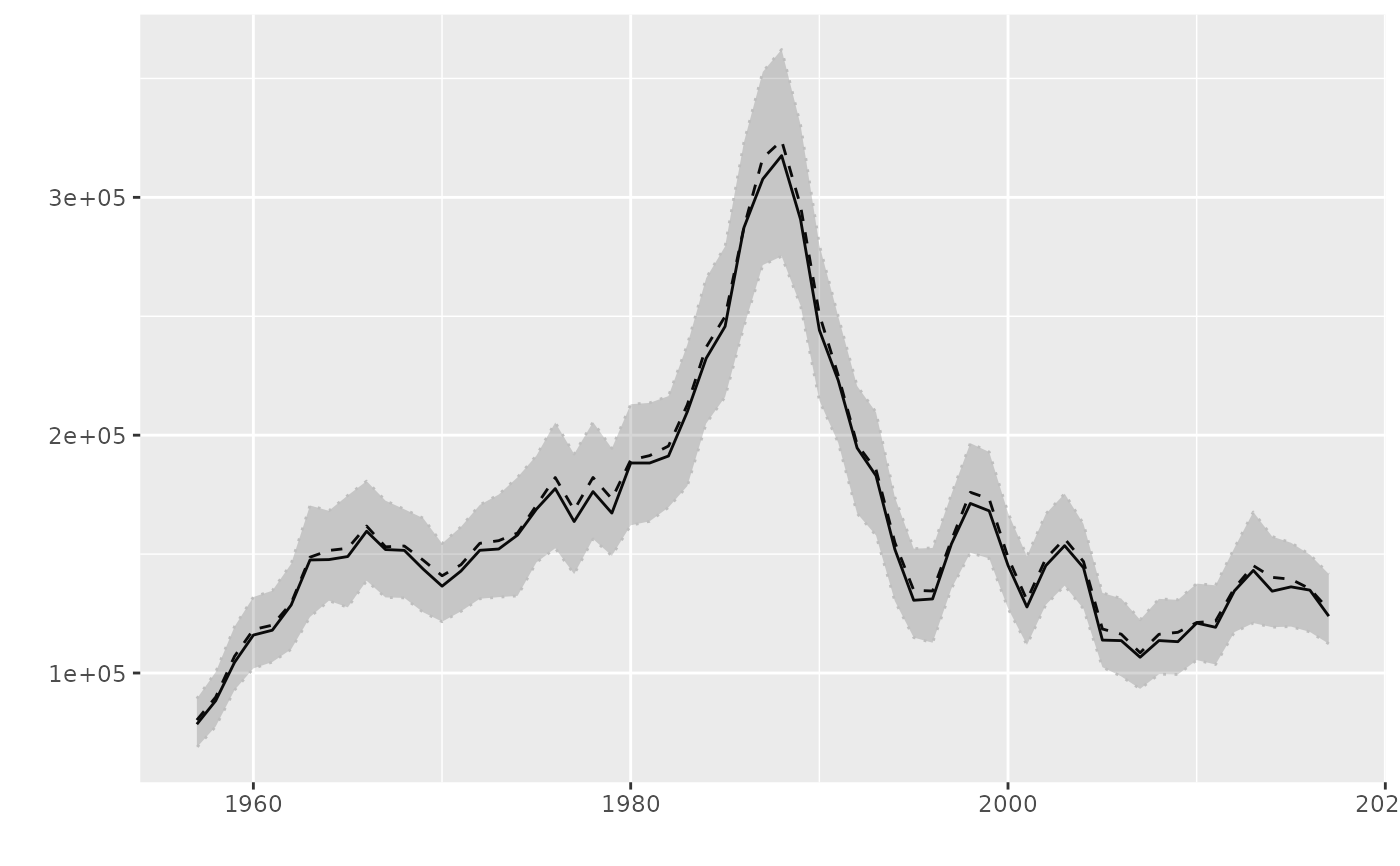 # plot for FLQuantPoint, FLQuant
plot(fqp, rlnorm(3, log(catch(ple4)), 0.20))
# plot for FLQuantPoint, FLQuant
plot(fqp, rlnorm(3, log(catch(ple4)), 0.20))
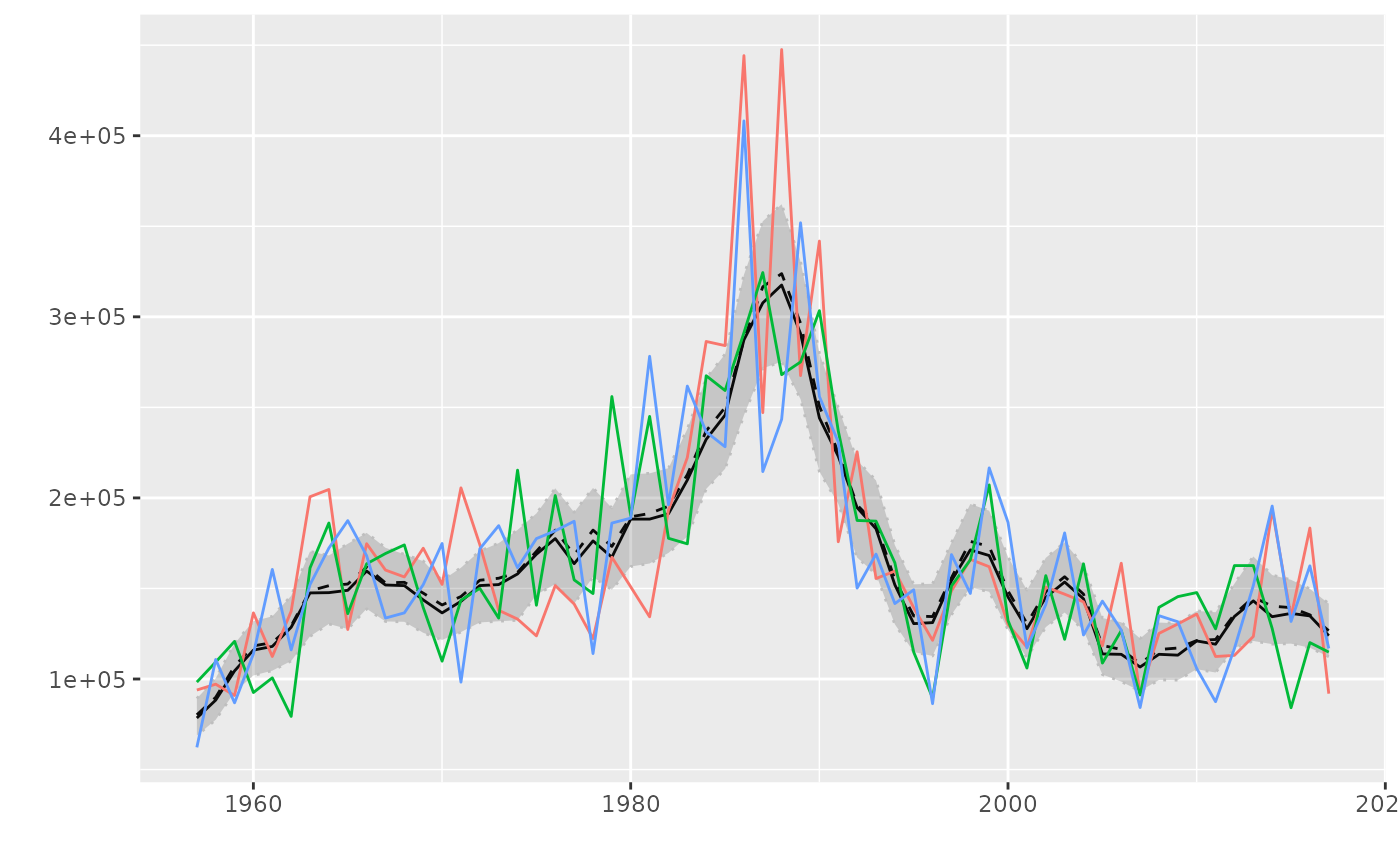 # plot for FLQuantPoint, FLQuants
fqp <- FLQuantPoint(rlnorm(300, log(catch(ple4)), 0.20))
fqs <- divide(rlnorm(3, log(catch(ple4)), 0.20))
plot(fqp, fqs)
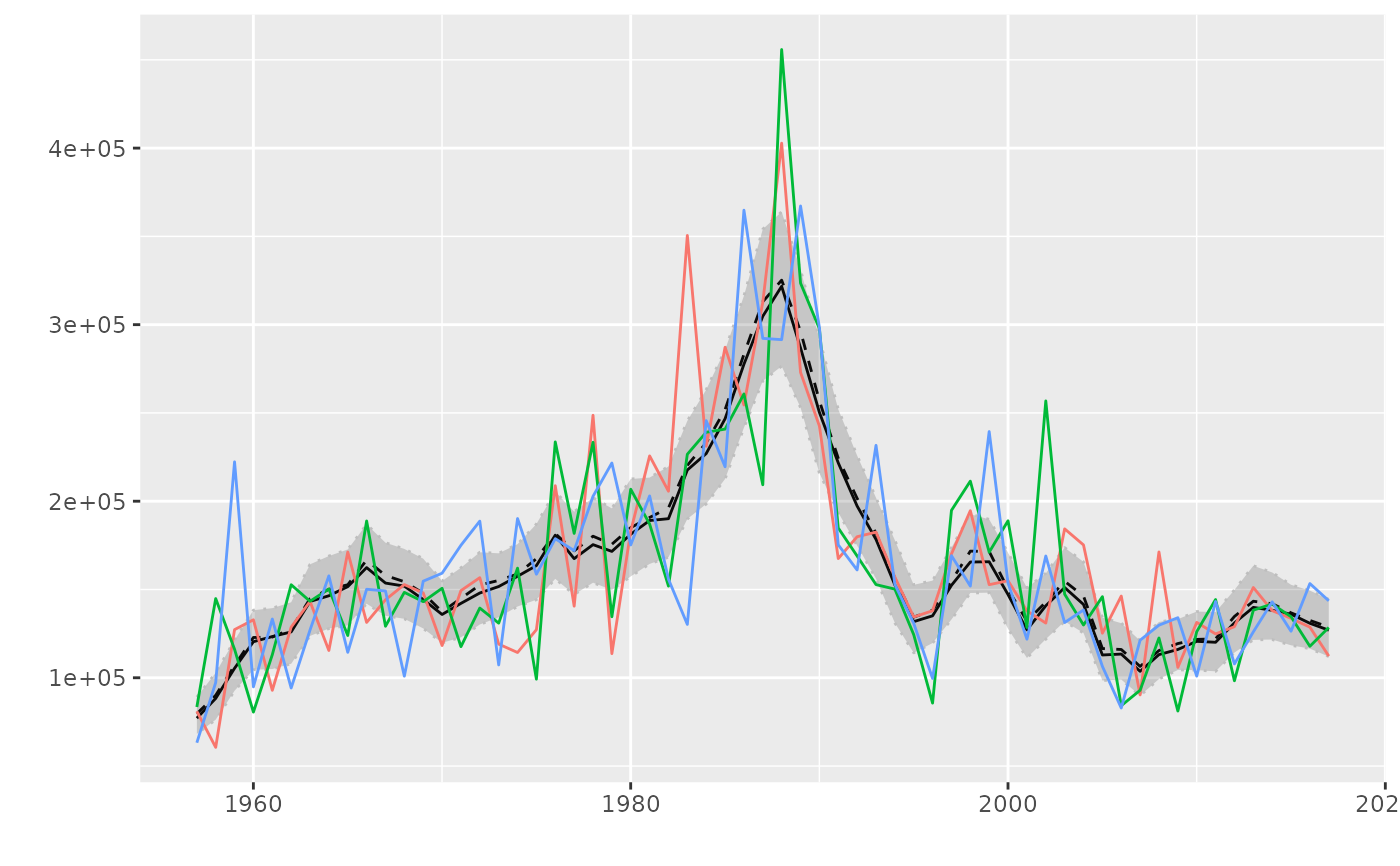
# plot for FLQuantPoint, FLQuants
fqp <- FLQuantPoint(rlnorm(300, log(catch(ple4)), 0.20))
fqs <- divide(rlnorm(3, log(catch(ple4)), 0.20))
plot(fqp, fqs)
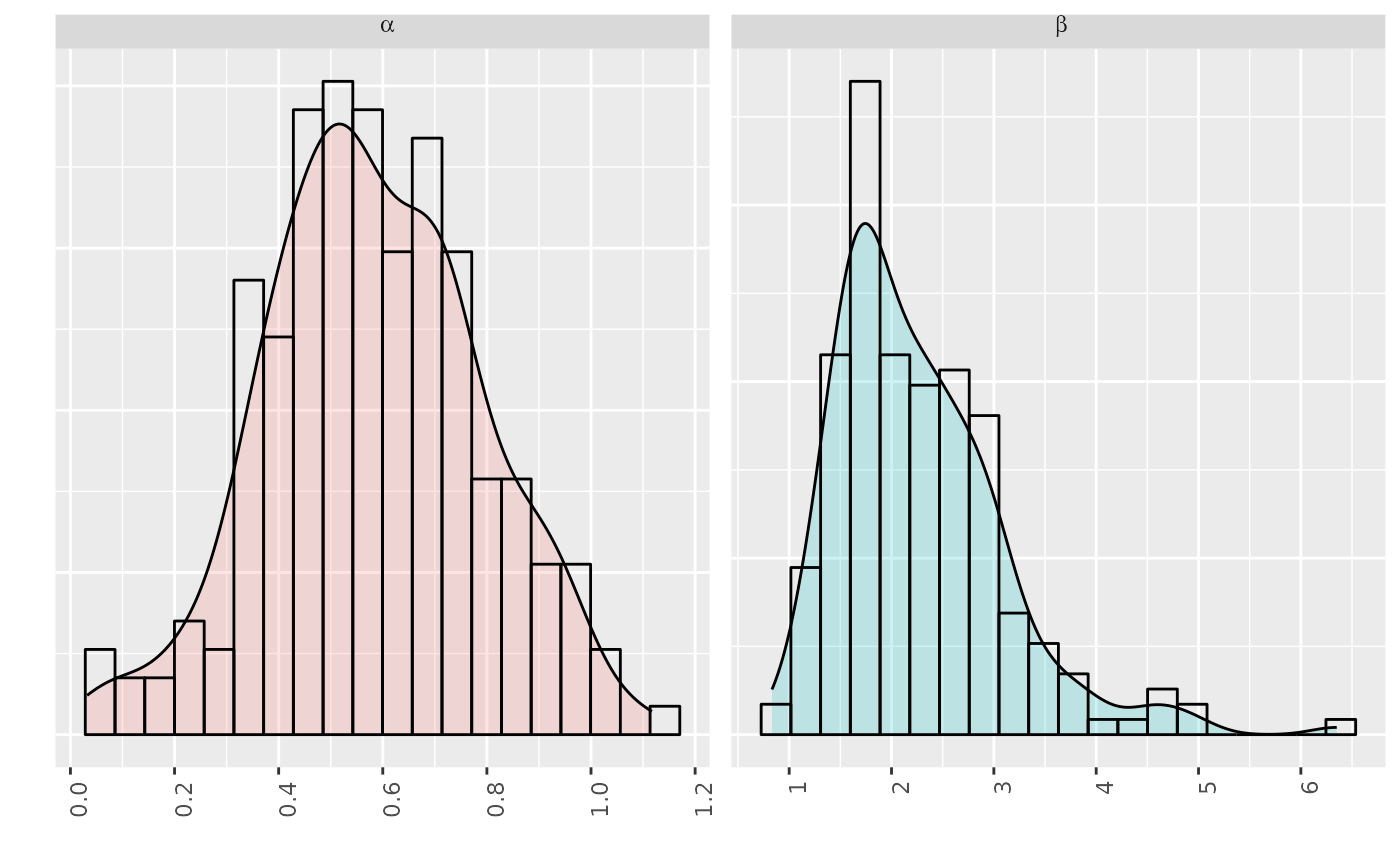
 par <- FLPar(alpha=rnorm(200, 0.6, 0.2), beta=rlnorm(200, 0.8, 0.3))
plot(par)
par <- FLPar(alpha=rnorm(200, 0.6, 0.2), beta=rlnorm(200, 0.8, 0.3))
plot(par)
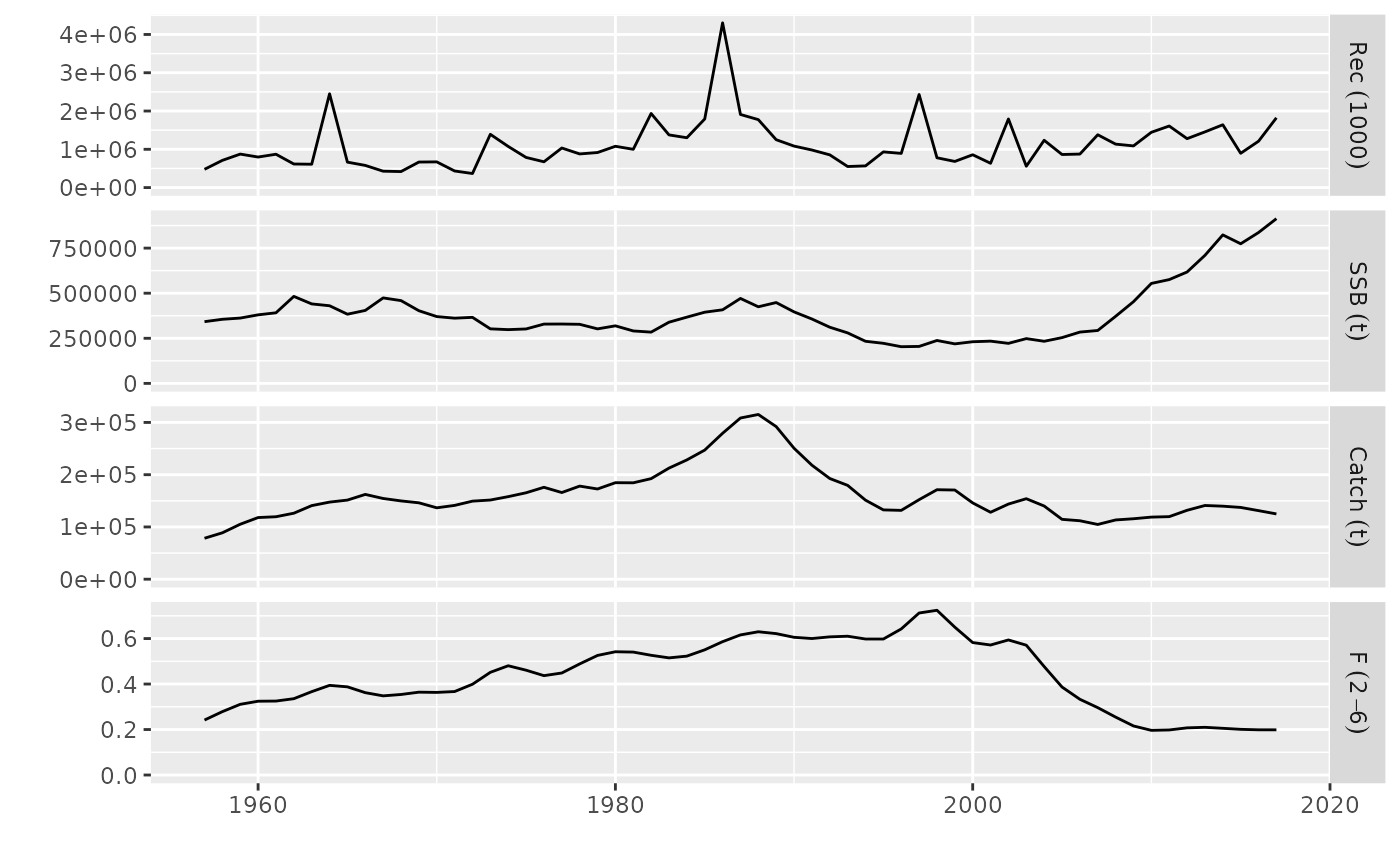
 # plot of an FLStock
data(ple4)
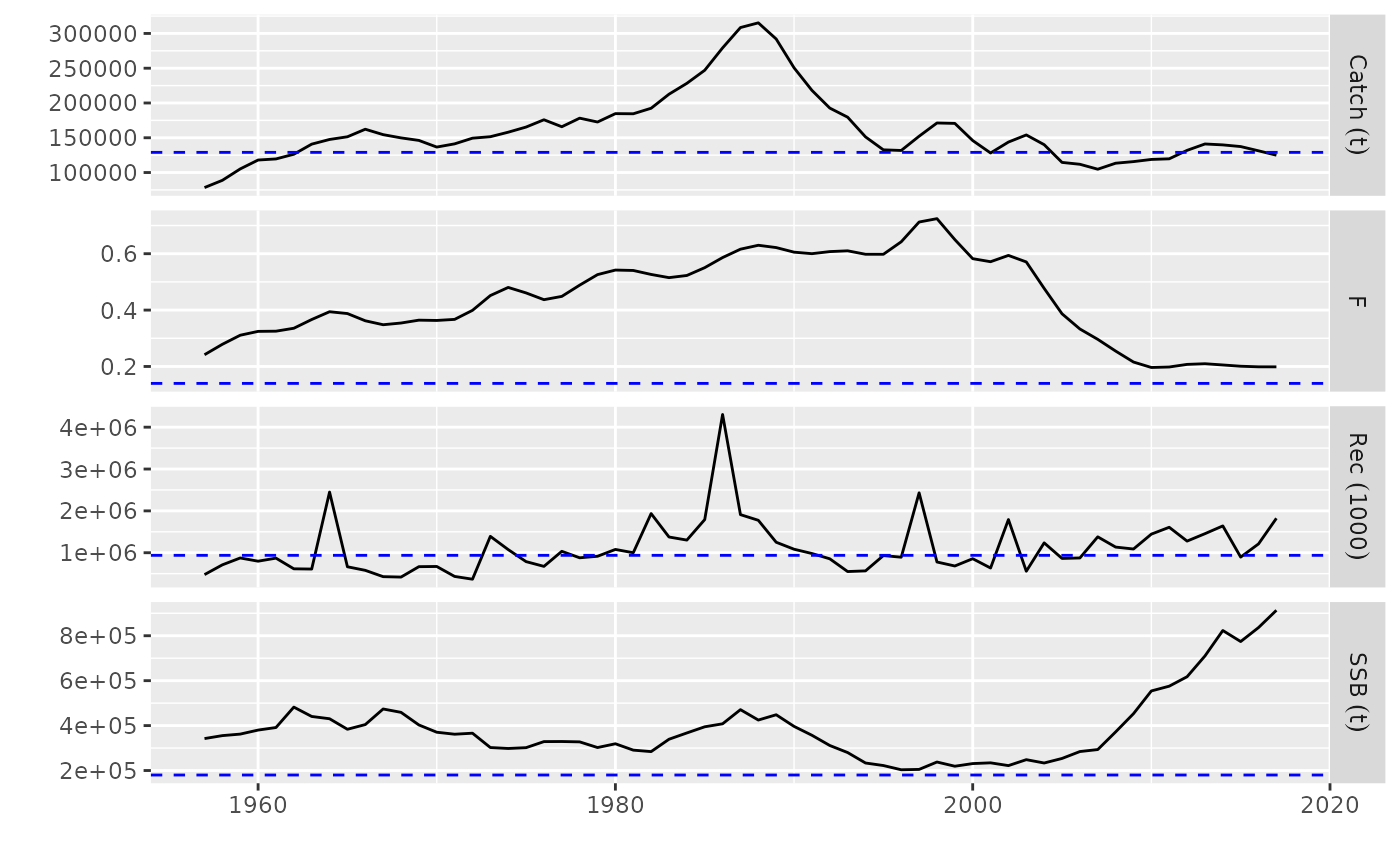
plot(ple4)
# plot of an FLStock
data(ple4)
plot(ple4)
 # plot for FLStock, FLPar
data(ple4)
rps <- FLPar(F=0.14, Catch=1.29e5, Rec=9.38e5, SSB=1.8e5)
plot(ple4, rps)
# plot for FLStock, FLPar
data(ple4)
rps <- FLPar(F=0.14, Catch=1.29e5, Rec=9.38e5, SSB=1.8e5)
plot(ple4, rps)
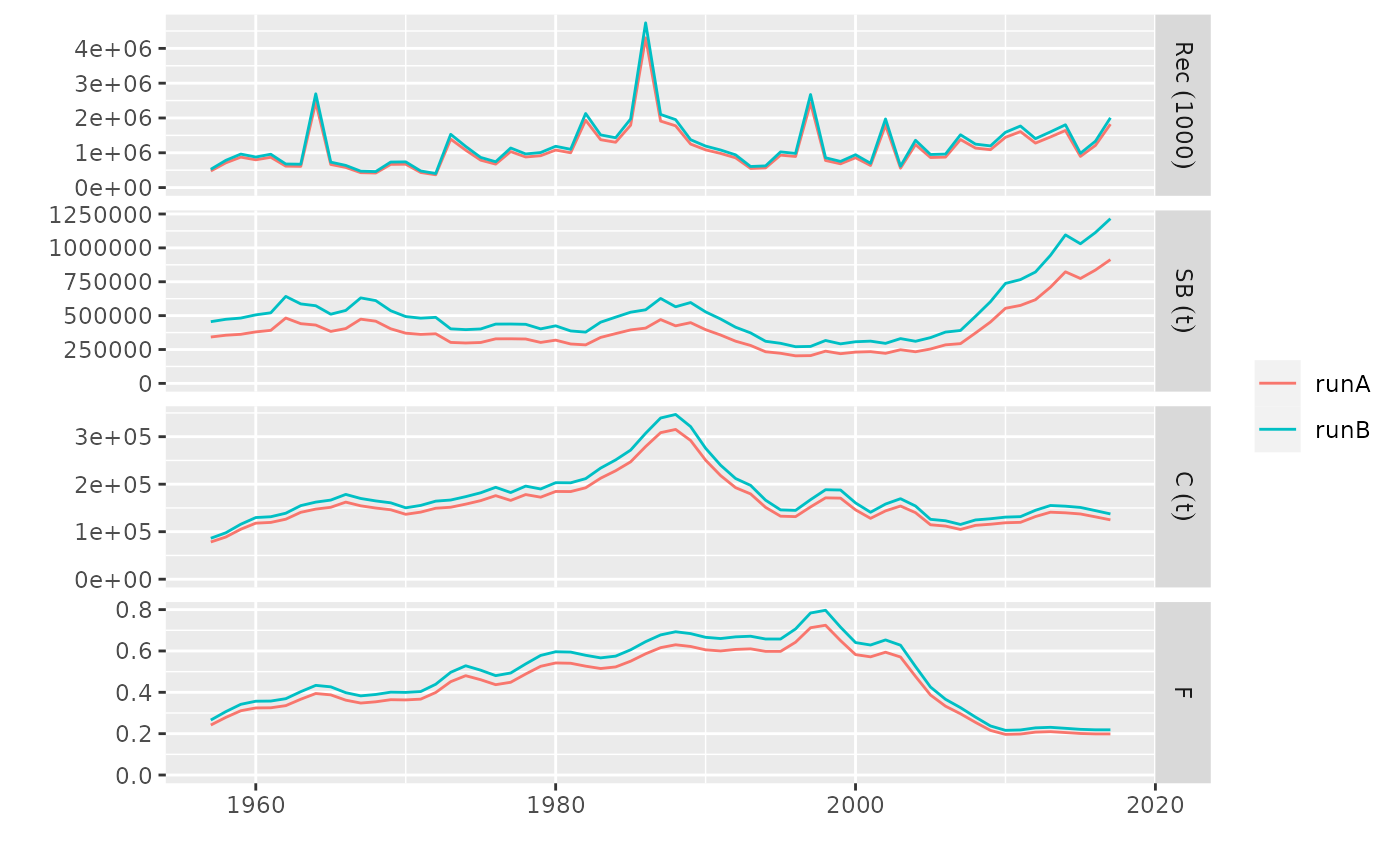
 # plot for FLStocks
data(ple4)
pls <- FLStocks(runA=ple4, runB=qapply(ple4, function(x) x*1.10))
plot(pls)
# plot for FLStocks
data(ple4)
pls <- FLStocks(runA=ple4, runB=qapply(ple4, function(x) x*1.10))
plot(pls)
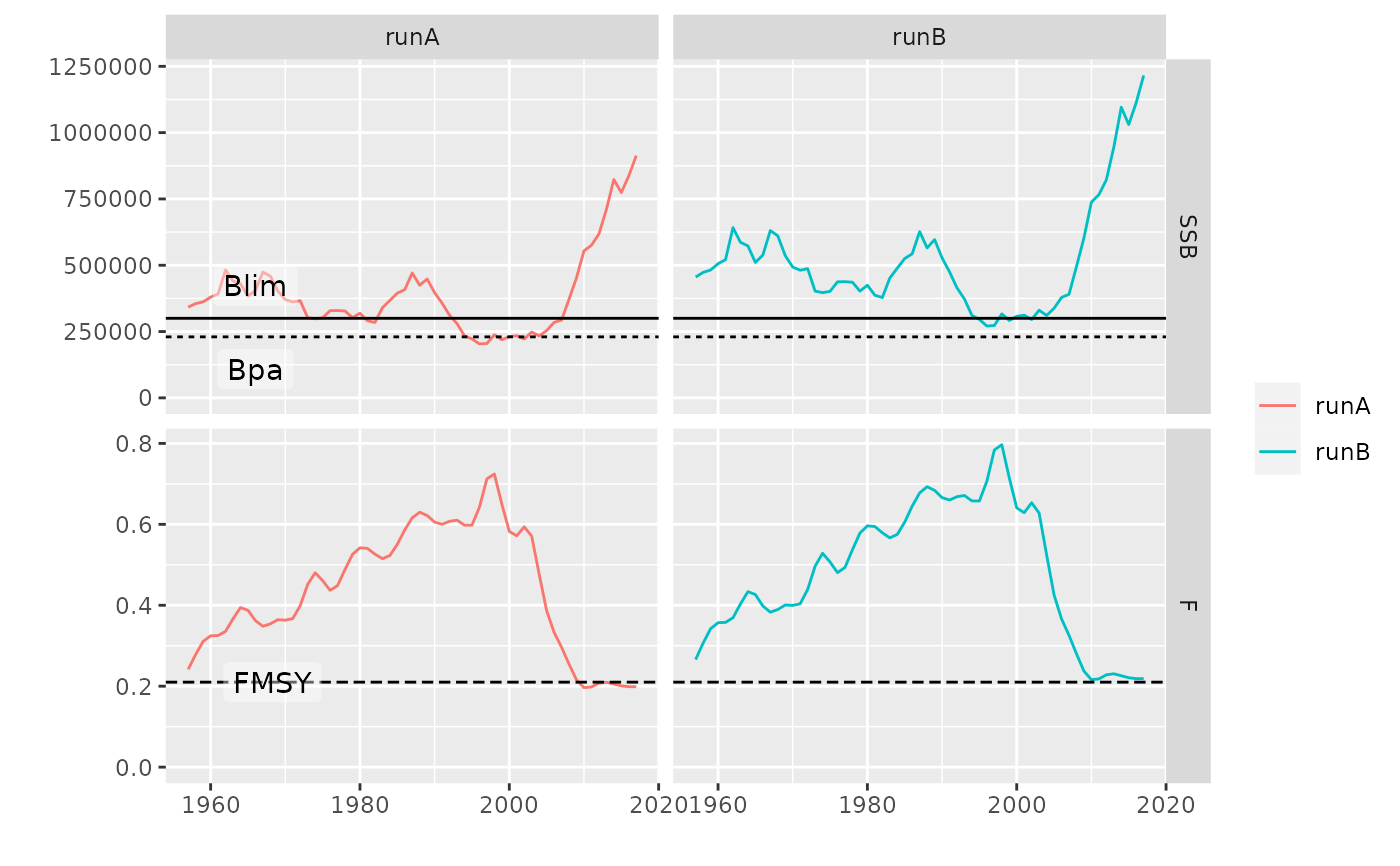
 # geom_flpar can be used draw refpts lines and labels
plot(pls, metrics=list(SSB=ssb, F=fbar)) +
facet_grid(qname~stock, scales='free') +
geom_flpar(data=FLPars(SSB=FLPar(Blim=300000, Bpa=230000),
F=FLPar(FMSY=0.21)), x=c(1960), stock='runA', fill=alpha('white', 0.4))
# geom_flpar can be used draw refpts lines and labels
plot(pls, metrics=list(SSB=ssb, F=fbar)) +
facet_grid(qname~stock, scales='free') +
geom_flpar(data=FLPars(SSB=FLPar(Blim=300000, Bpa=230000),
F=FLPar(FMSY=0.21)), x=c(1960), stock='runA', fill=alpha('white', 0.4))
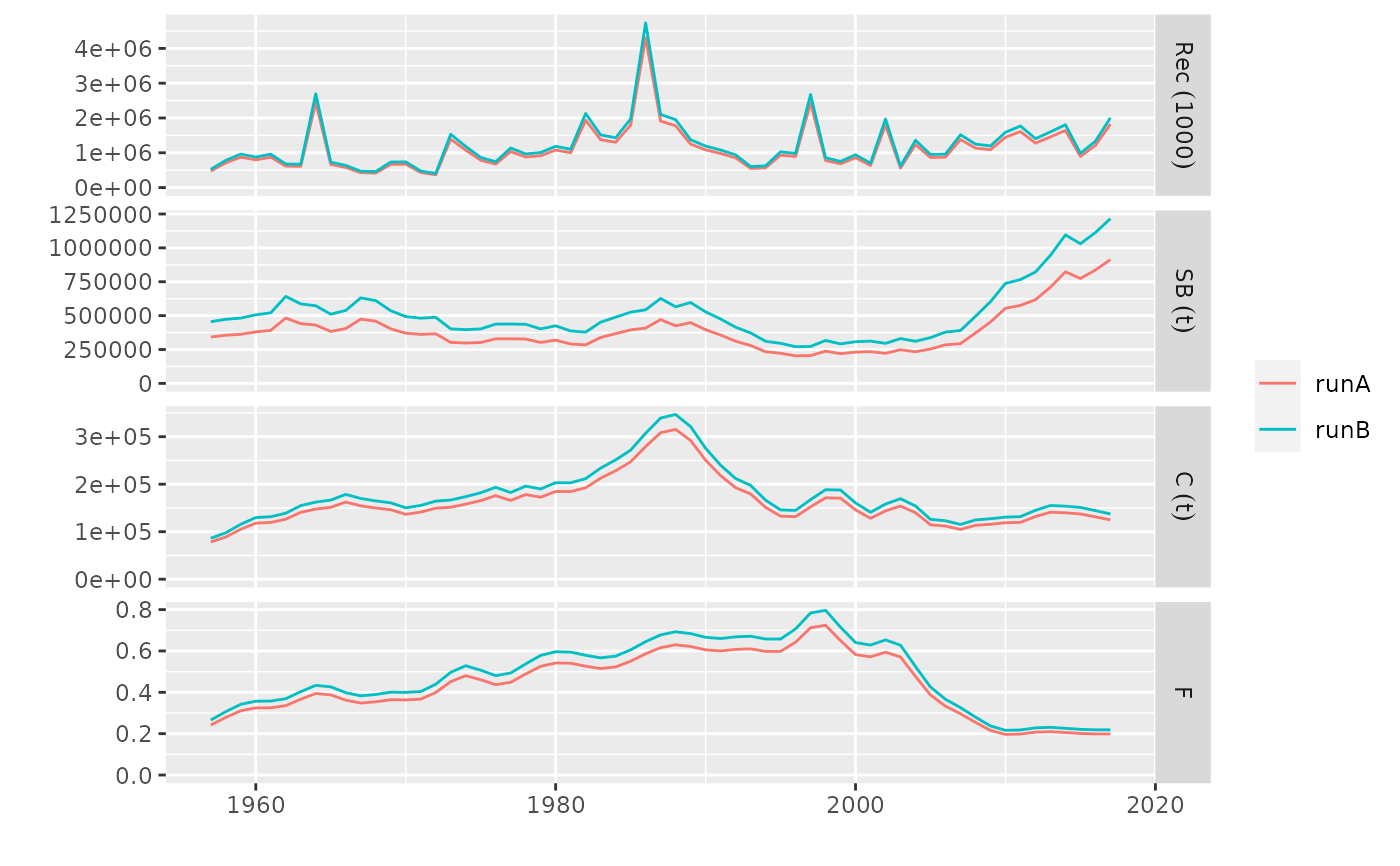
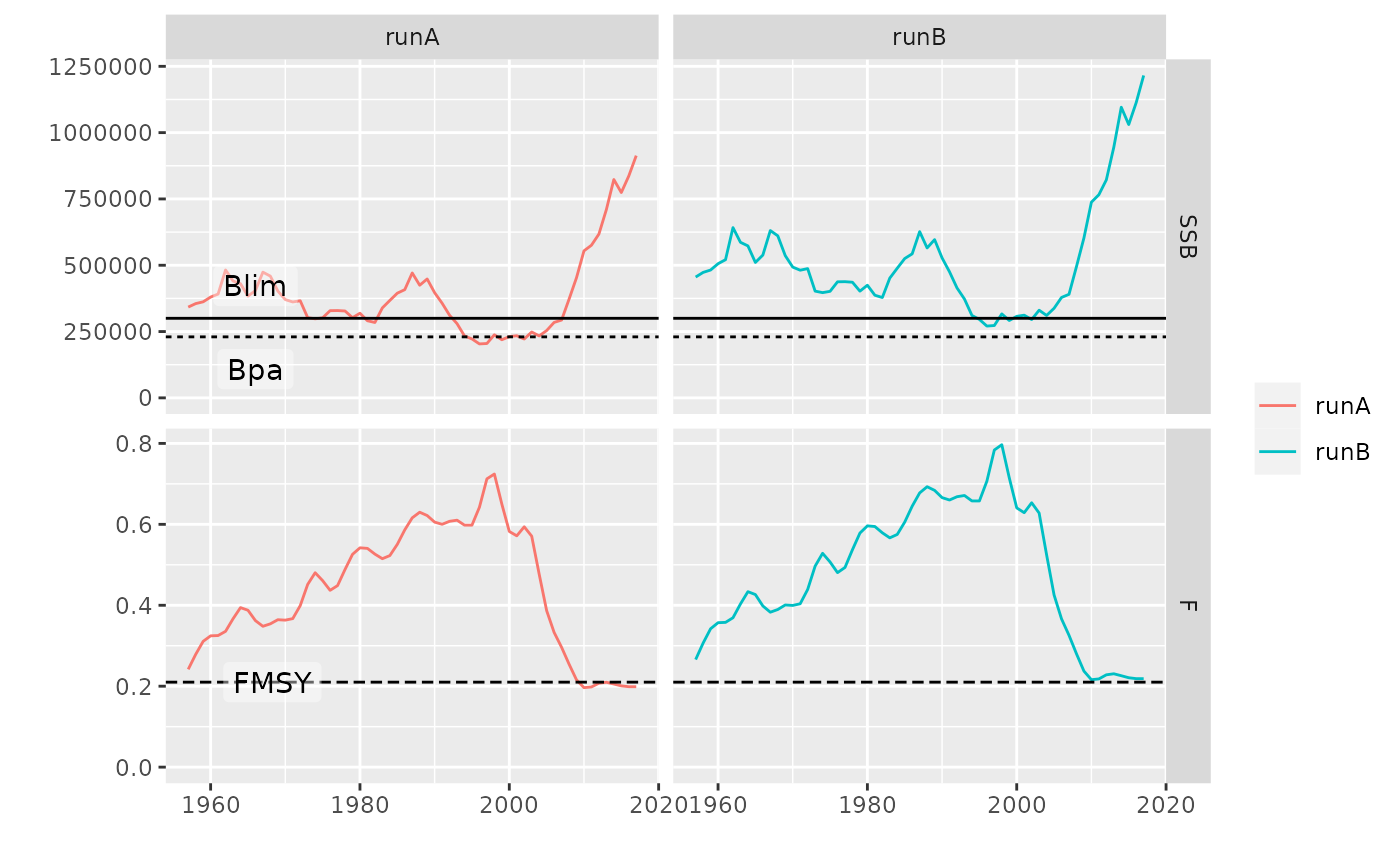
 # plot for FLStocks
data(ple4)
pls <- FLStocks(runA=ple4, runB=qapply(ple4, function(x) x*1.10))
plot(pls)
# plot for FLStocks
data(ple4)
pls <- FLStocks(runA=ple4, runB=qapply(ple4, function(x) x*1.10))
plot(pls)
 # geom_flpar can then be used draw refpts lines and labels
plot(pls, metrics=list(SSB=ssb, F=fbar)) +
facet_grid(qname~stock, scales='free') +
geom_flpar(data=FLPars(SSB=FLPar(Blim=300000, Bpa=230000),
F=FLPar(FMSY=0.21)), x=c(1960), stock='runA', fill=alpha('white', 0.4))
# geom_flpar can then be used draw refpts lines and labels
plot(pls, metrics=list(SSB=ssb, F=fbar)) +
facet_grid(qname~stock, scales='free') +
geom_flpar(data=FLPars(SSB=FLPar(Blim=300000, Bpa=230000),
F=FLPar(FMSY=0.21)), x=c(1960), stock='runA', fill=alpha('white', 0.4))
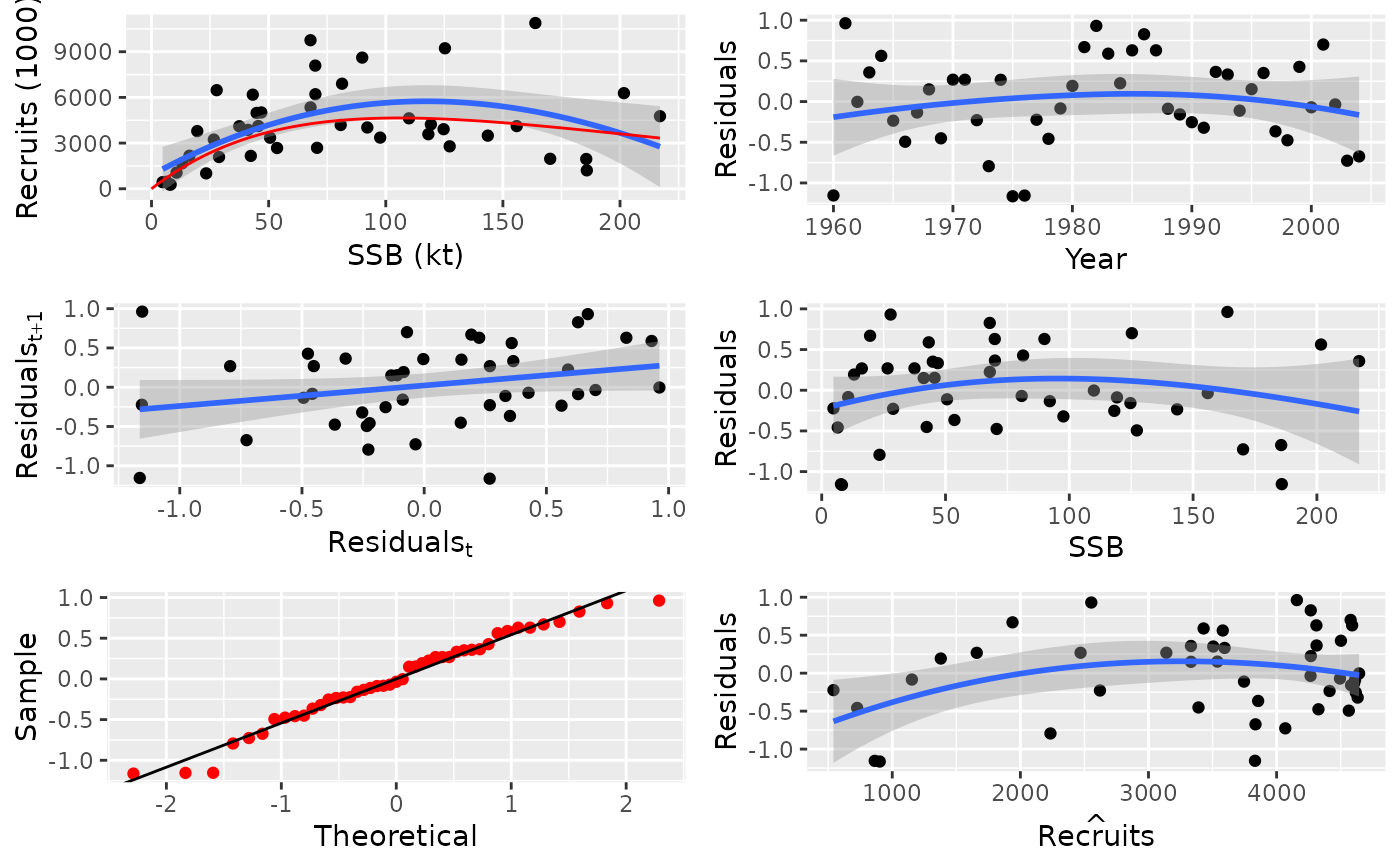
 # plot for FLSR
data(nsher)
plot(nsher)
# plot for FLSR
data(nsher)
plot(nsher)
 # plot for FLSRs
data(nsher)
srs <- FLSRs(sapply(c('segreg', 'bevholt'), function(x) {
y <- nsher
model(y) <- x
return(fmle(y))
}))
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -14.190173
#> Scaled convergence tolerance is 2.1145e-07
#> Stepsize computed as 6.789002
#> BUILD 3 -13.430599 -15.242851
#> EXTENSION 5 -14.190173 -16.074769
#> EXTENSION 7 -15.242851 -17.135003
#> HI-REDUCTION 9 -16.074769 -17.135003
#> LO-REDUCTION 11 -16.401987 -17.135003
#> LO-REDUCTION 13 -16.738659 -17.135003
#> HI-REDUCTION 15 -16.967762 -17.135003
#> HI-REDUCTION 17 -16.990440 -17.135003
#> LO-REDUCTION 19 -17.053124 -17.135003
#> LO-REDUCTION 21 -17.107715 -17.135003
#> REFLECTION 23 -17.132087 -17.139431
#> HI-REDUCTION 25 -17.135003 -17.139841
#> HI-REDUCTION 27 -17.139431 -17.140713
#> HI-REDUCTION 29 -17.139841 -17.142261
#> LO-REDUCTION 31 -17.140713 -17.142261
#> LO-REDUCTION 33 -17.141732 -17.142261
#> HI-REDUCTION 35 -17.141925 -17.142261
#> LO-REDUCTION 37 -17.142098 -17.142261
#> LO-REDUCTION 39 -17.142233 -17.142261
#> HI-REDUCTION 41 -17.142238 -17.142265
#> LO-REDUCTION 43 -17.142261 -17.142268
#> HI-REDUCTION 45 -17.142265 -17.142270
#> HI-REDUCTION 47 -17.142268 -17.142271
#> HI-REDUCTION 49 -17.142270 -17.142271
#> HI-REDUCTION 51 -17.142270 -17.142271
#> Exiting from Nelder Mead minimizer
#> 53 function evaluations used
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -10.336211
#> Scaled convergence tolerance is 1.54022e-07
#> Stepsize computed as 501.110000
#> BUILD 3 44.842344 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 5 31.685209 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 7 17.913114 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 9 5.415279 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 11 -3.412974 -11.603908
#> HI-REDUCTION 13 -8.018030 -11.603908
#> LO-REDUCTION 15 -10.336211 -11.603908
#> LO-REDUCTION 17 -11.081040 -11.603908
#> EXTENSION 19 -11.295930 -12.061705
#> LO-REDUCTION 21 -11.603908 -12.061705
#> REFLECTION 23 -11.813826 -12.087620
#> REFLECTION 25 -12.061705 -12.199591
#> LO-REDUCTION 27 -12.087620 -12.199591
#> LO-REDUCTION 29 -12.158184 -12.199591
#> LO-REDUCTION 31 -12.191726 -12.199591
#> HI-REDUCTION 33 -12.192269 -12.199591
#> HI-REDUCTION 35 -12.197784 -12.199591
#> LO-REDUCTION 37 -12.198015 -12.199591
#> HI-REDUCTION 39 -12.199555 -12.199776
#> REFLECTION 41 -12.199591 -12.200058
#> HI-REDUCTION 43 -12.199776 -12.200092
#> HI-REDUCTION 45 -12.200058 -12.200142
#> HI-REDUCTION 47 -12.200092 -12.200155
#> HI-REDUCTION 49 -12.200142 -12.200160
#> HI-REDUCTION 51 -12.200155 -12.200177
#> HI-REDUCTION 53 -12.200160 -12.200177
#> LO-REDUCTION 55 -12.200171 -12.200179
#> HI-REDUCTION 57 -12.200177 -12.200179
#> HI-REDUCTION 59 -12.200178 -12.200179
#> HI-REDUCTION 61 -12.200179 -12.200179
#> HI-REDUCTION 63 -12.200179 -12.200179
#> HI-REDUCTION 65 -12.200179 -12.200179
#> Exiting from Nelder Mead minimizer
#> 67 function evaluations used
plot(srs, facets=TRUE)
#> Error in seq.default(0, max(dat[dat$sr == i, "ssb"]), length = 100): 'to' must be a finite number
plot(srs, legend_label=eqlabel)
# plot for FLSRs
data(nsher)
srs <- FLSRs(sapply(c('segreg', 'bevholt'), function(x) {
y <- nsher
model(y) <- x
return(fmle(y))
}))
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -14.190173
#> Scaled convergence tolerance is 2.1145e-07
#> Stepsize computed as 6.789002
#> BUILD 3 -13.430599 -15.242851
#> EXTENSION 5 -14.190173 -16.074769
#> EXTENSION 7 -15.242851 -17.135003
#> HI-REDUCTION 9 -16.074769 -17.135003
#> LO-REDUCTION 11 -16.401987 -17.135003
#> LO-REDUCTION 13 -16.738659 -17.135003
#> HI-REDUCTION 15 -16.967762 -17.135003
#> HI-REDUCTION 17 -16.990440 -17.135003
#> LO-REDUCTION 19 -17.053124 -17.135003
#> LO-REDUCTION 21 -17.107715 -17.135003
#> REFLECTION 23 -17.132087 -17.139431
#> HI-REDUCTION 25 -17.135003 -17.139841
#> HI-REDUCTION 27 -17.139431 -17.140713
#> HI-REDUCTION 29 -17.139841 -17.142261
#> LO-REDUCTION 31 -17.140713 -17.142261
#> LO-REDUCTION 33 -17.141732 -17.142261
#> HI-REDUCTION 35 -17.141925 -17.142261
#> LO-REDUCTION 37 -17.142098 -17.142261
#> LO-REDUCTION 39 -17.142233 -17.142261
#> HI-REDUCTION 41 -17.142238 -17.142265
#> LO-REDUCTION 43 -17.142261 -17.142268
#> HI-REDUCTION 45 -17.142265 -17.142270
#> HI-REDUCTION 47 -17.142268 -17.142271
#> HI-REDUCTION 49 -17.142270 -17.142271
#> HI-REDUCTION 51 -17.142270 -17.142271
#> Exiting from Nelder Mead minimizer
#> 53 function evaluations used
#> Nelder-Mead direct search function minimizer
#> function value for initial parameters = -10.336211
#> Scaled convergence tolerance is 1.54022e-07
#> Stepsize computed as 501.110000
#> BUILD 3 44.842344 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 5 31.685209 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 7 17.913114 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 9 5.415279 -11.603908
#> Warning: NaNs produced
#> HI-REDUCTION 11 -3.412974 -11.603908
#> HI-REDUCTION 13 -8.018030 -11.603908
#> LO-REDUCTION 15 -10.336211 -11.603908
#> LO-REDUCTION 17 -11.081040 -11.603908
#> EXTENSION 19 -11.295930 -12.061705
#> LO-REDUCTION 21 -11.603908 -12.061705
#> REFLECTION 23 -11.813826 -12.087620
#> REFLECTION 25 -12.061705 -12.199591
#> LO-REDUCTION 27 -12.087620 -12.199591
#> LO-REDUCTION 29 -12.158184 -12.199591
#> LO-REDUCTION 31 -12.191726 -12.199591
#> HI-REDUCTION 33 -12.192269 -12.199591
#> HI-REDUCTION 35 -12.197784 -12.199591
#> LO-REDUCTION 37 -12.198015 -12.199591
#> HI-REDUCTION 39 -12.199555 -12.199776
#> REFLECTION 41 -12.199591 -12.200058
#> HI-REDUCTION 43 -12.199776 -12.200092
#> HI-REDUCTION 45 -12.200058 -12.200142
#> HI-REDUCTION 47 -12.200092 -12.200155
#> HI-REDUCTION 49 -12.200142 -12.200160
#> HI-REDUCTION 51 -12.200155 -12.200177
#> HI-REDUCTION 53 -12.200160 -12.200177
#> LO-REDUCTION 55 -12.200171 -12.200179
#> HI-REDUCTION 57 -12.200177 -12.200179
#> HI-REDUCTION 59 -12.200178 -12.200179
#> HI-REDUCTION 61 -12.200179 -12.200179
#> HI-REDUCTION 63 -12.200179 -12.200179
#> HI-REDUCTION 65 -12.200179 -12.200179
#> Exiting from Nelder Mead minimizer
#> 67 function evaluations used
plot(srs, facets=TRUE)
#> Error in seq.default(0, max(dat[dat$sr == i, "ssb"]), length = 100): 'to' must be a finite number
plot(srs, legend_label=eqlabel)
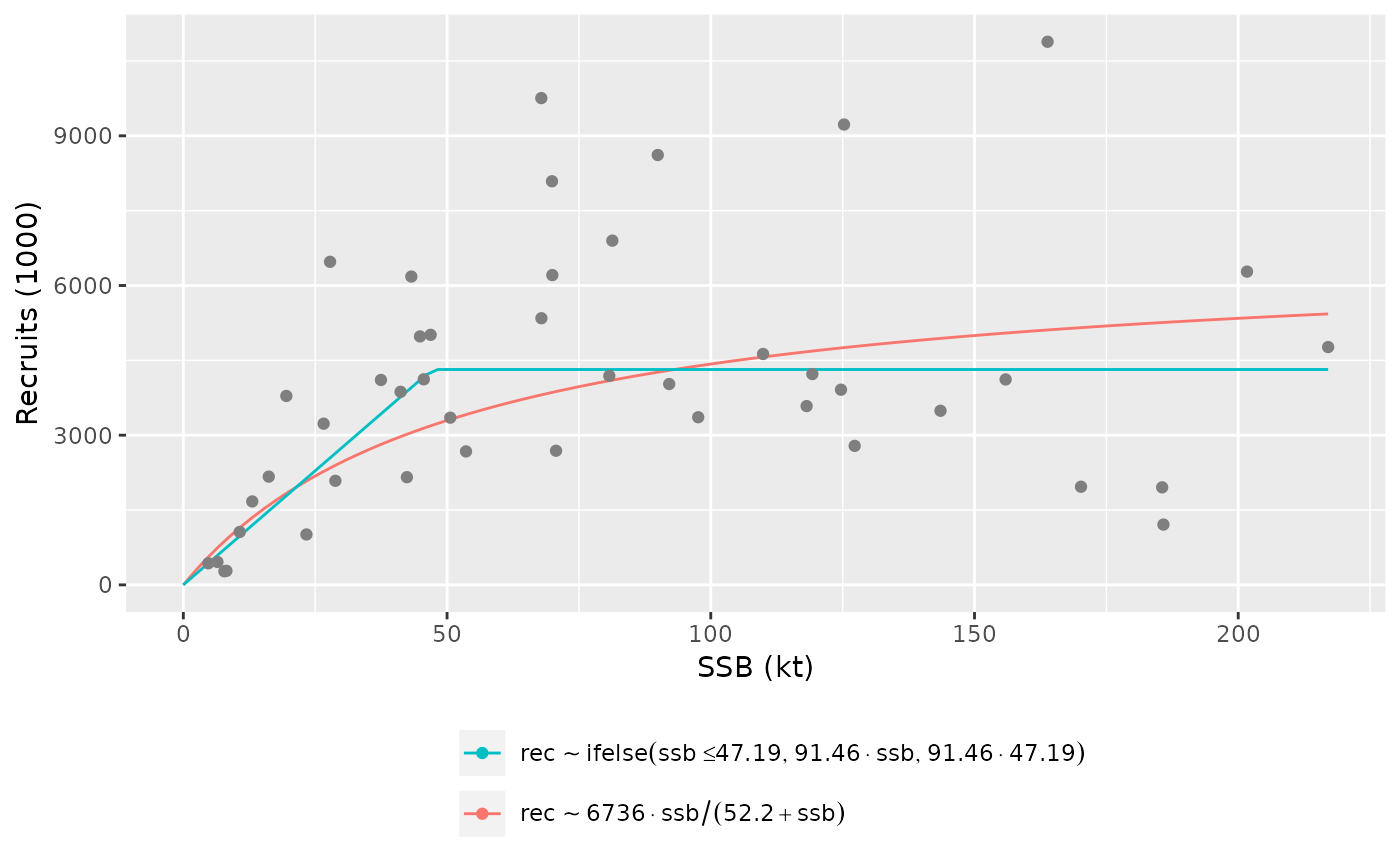 plot(srs, legend_label=modlabel)
plot(srs, legend_label=modlabel)
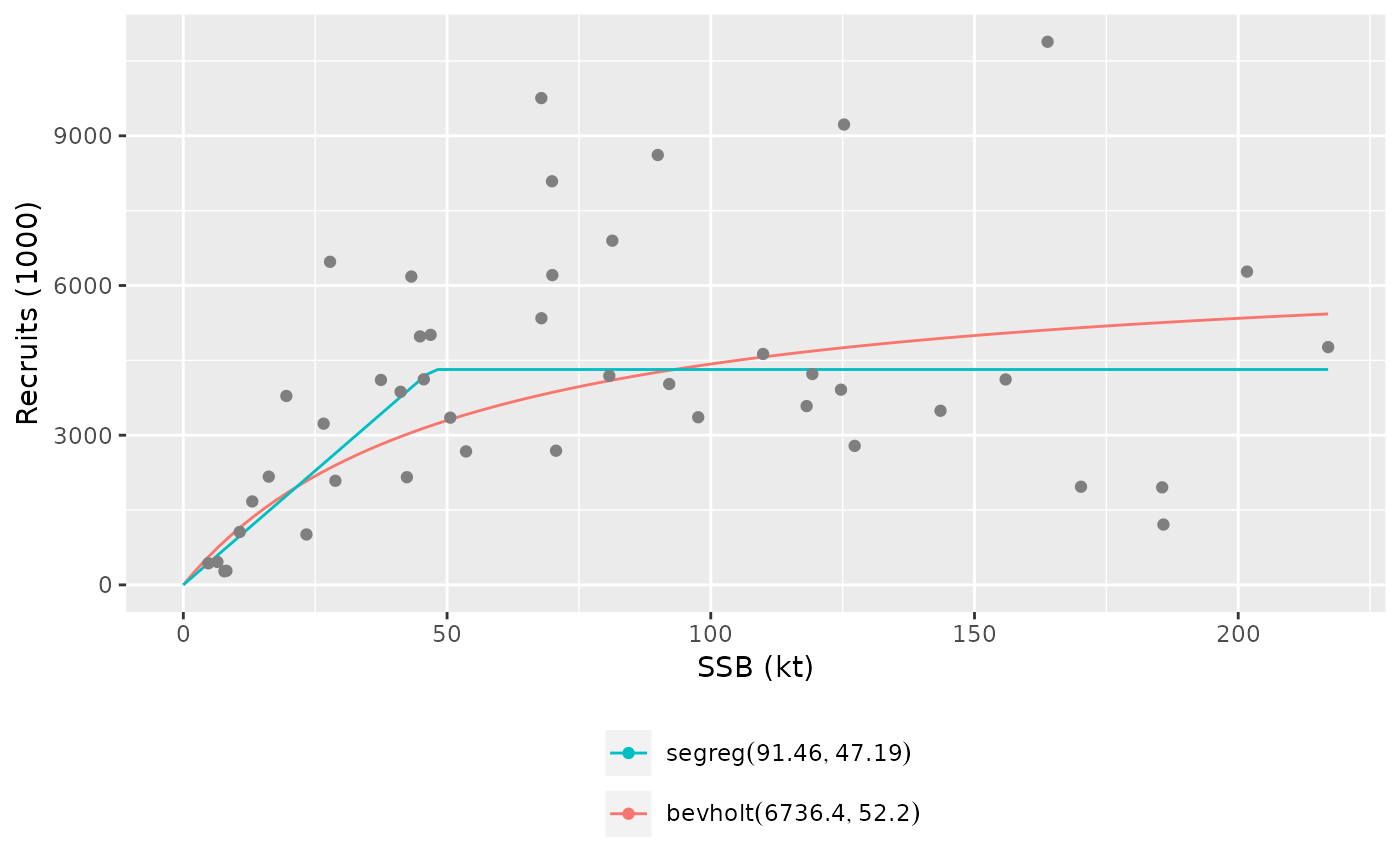 # Plot a FLIndex object
data(ple4.index)
plot(ple4.index)
# Plot a FLIndex object
data(ple4.index)
plot(ple4.index)
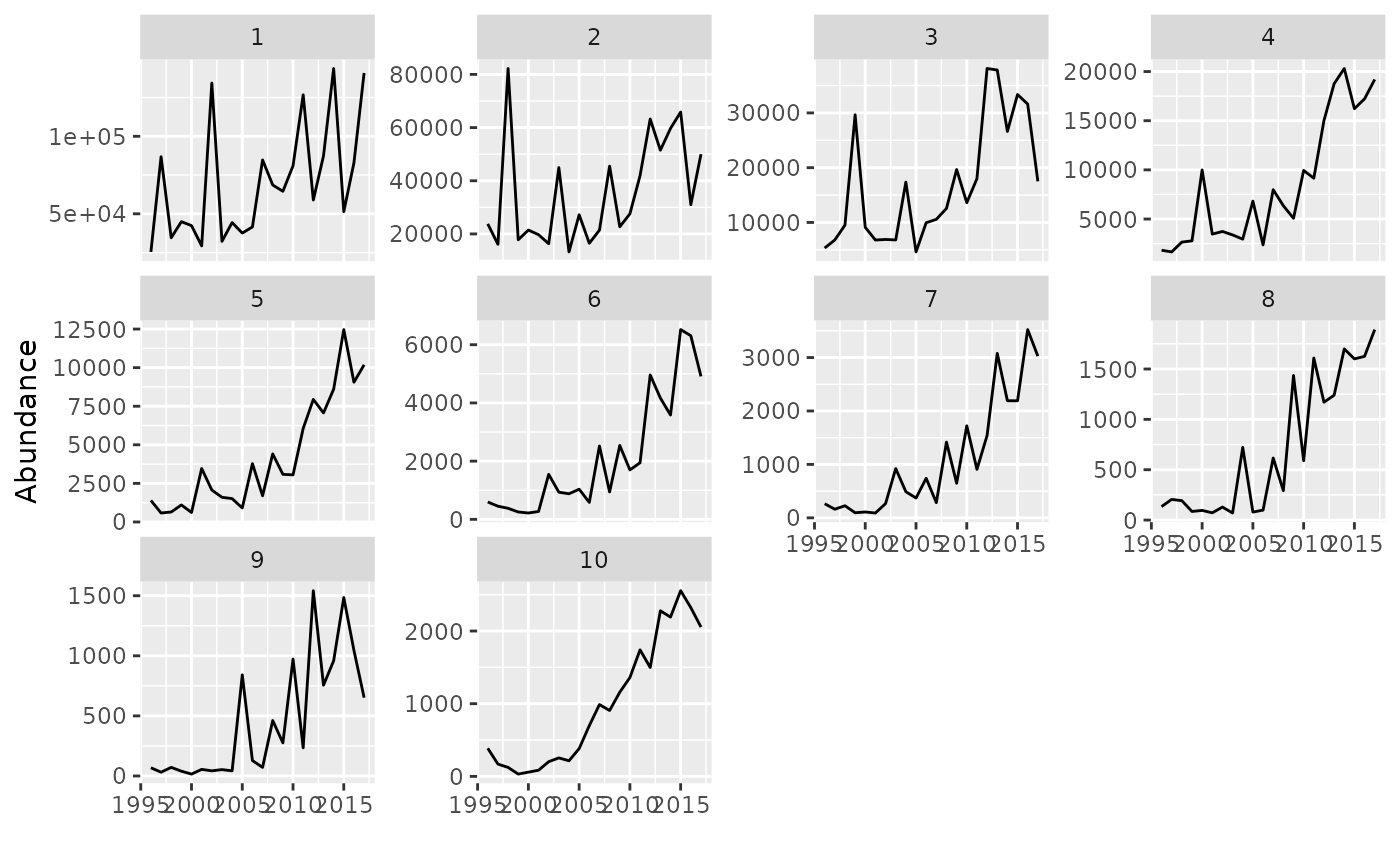 # Plot a FLIndices object
data(ple4.indices)
plot(ple4.indices)
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
# Plot a FLIndices object
data(ple4.indices)
plot(ple4.indices)
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
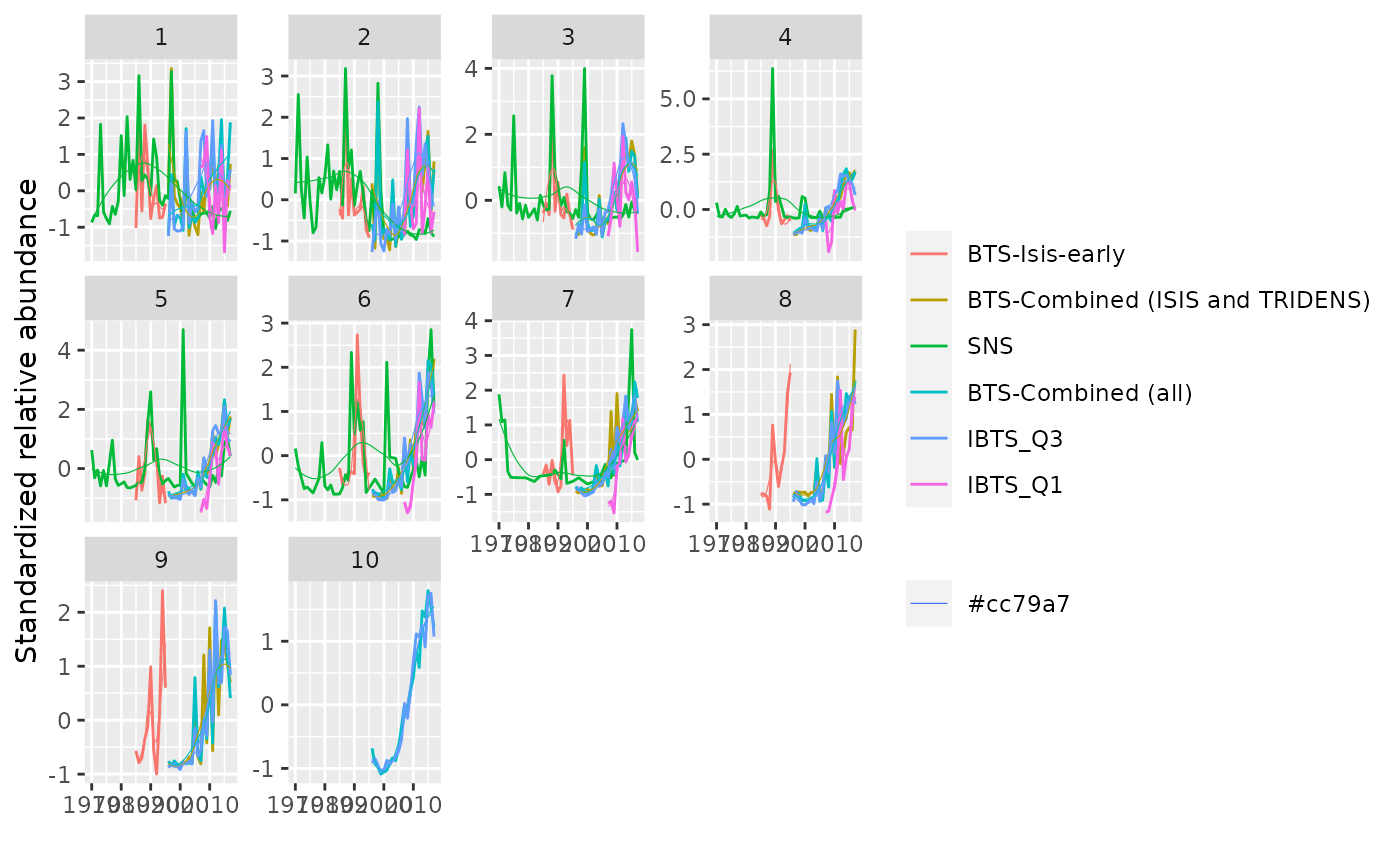
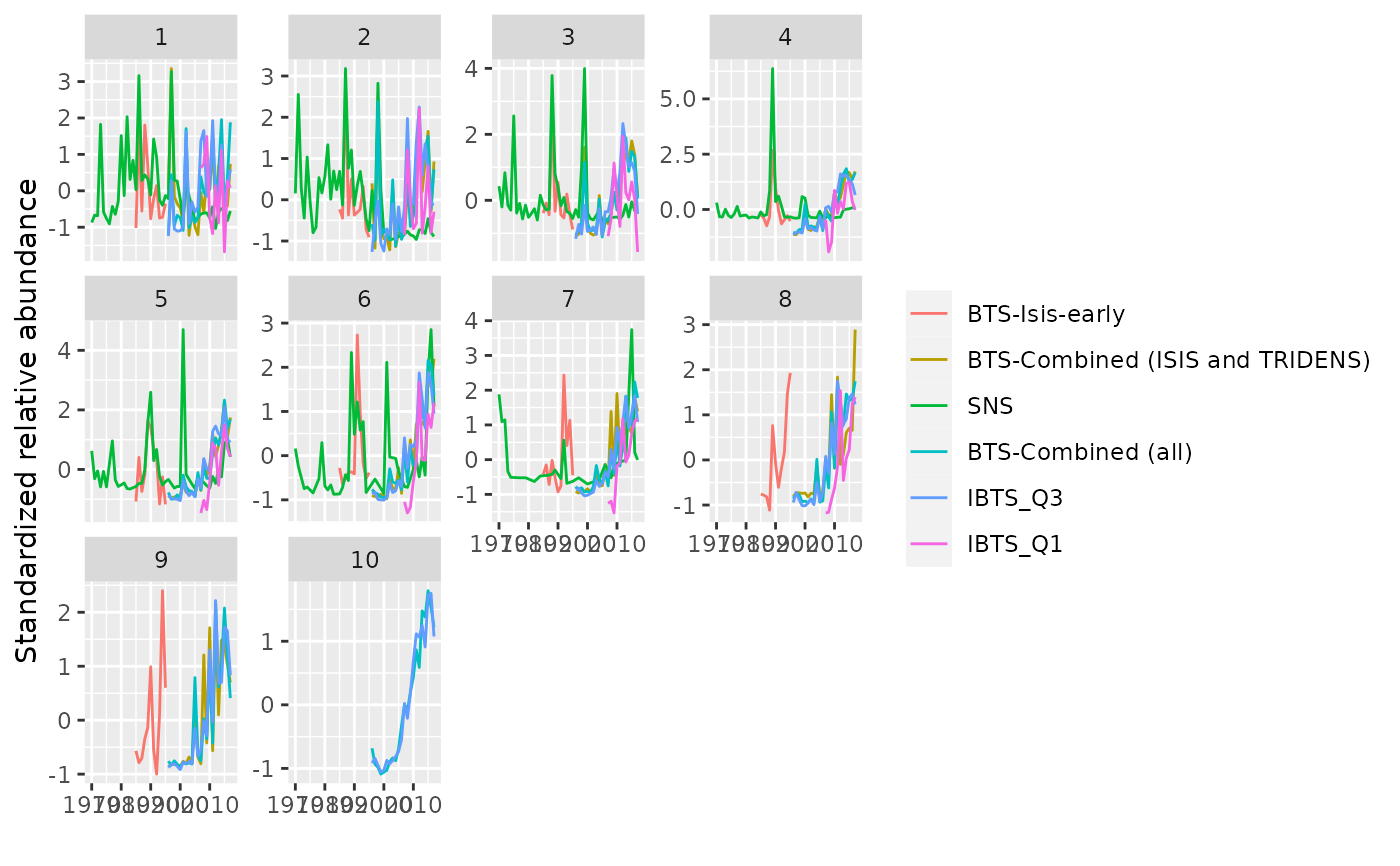 plot(ple4.indices) +
geom_smooth(formula=y ~ x, se=FALSE, method="loess", linewidth=0.2)
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_smooth()`).
plot(ple4.indices) +
geom_smooth(formula=y ~ x, se=FALSE, method="loess", linewidth=0.2)
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_fl_quantiles()`).
#> Warning: Removed 43 rows containing non-finite values (`stat_smooth()`).